Por que PESO não deve ser tomado como sinônimo de FORÇA GRAVITACIONAL?

10 de agosto, 2014 às 17:54 | Postado em Forças inerciais, Forma da Terra, Gravitação, Mecânica

Prezado colega professor Lang

Gostaria de compartilhar um debate que tive.

Para você, PESO É SINÔNIMO de força gravitacional? Ele varia com o inverso do quadrado da distancia e é diretamente proporcional ao produto das massas ? Tive um debate com um colega e gostaria de poder ouvir o seu ponto de vista.

Historicamente o conceito de PESO está comprometido com as operações de PESAGEM, com os procedimentos através dos quais desde épocas remotas os homens pesam coisas.

A partir da Mecânica Newtoniana o conceito de FORÇA GRAVITACIONAL está bem estabelecido na Lei da Gravitação Universal.

Entretanto não se deve confundir PESO com FORÇA GRAVITACIONAL sob pena de invalidar todos os processos que reconhecidamente são realizados em pesagens conforme discuto mais adiante. Há uma definição de PESO como a força que impede que um corpo esteja em queda livre (por exemplo: Weight). Neste caso o PESO seria uma força PARA CIMA, em sentido contrário ao da orientação da aceleração de queda livre local.

Parece ser a definição mais usual aquela que diz que o PESO é o produto da massa pela aceleração de queda livre local (também chamada de aceleração da gravidade). Esta é a definição que se encontra na ISO 80000-4 (2006). Abaixo está a definição.

Definition

,

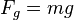where m is mass and g is local acceleration of free fall.

Remarks

• It should be noted that, when the reference frame is Earth, this quantity comprises not only the local gravitational force, but also the local centrifugal force due to the rotation of the Earth, a force which varies with latitude.
• The effect of atmospheric buoyancy is excluded in the weight.
• In common parlance, the name “weight” continues to be used where “mass” is meant, but this practice is deprecated.

                                                         — ISO 80000-4 (2006)

É bem sabido que a aceleração de queda livre local NÃO é idêntica à intensidade do campo gravitacional pois qualquer sistema de referência solidário à Terra (exceção feita quando consideramos pontos sobre o eixo de rotação  do nosso planeta) é um sistema não inercial, acelerado devido à rotação do planeta. Vide por exemplo em Diferença na aceleração da gravidade do polo para o equador.

Desta forma se tomarmos PESO como sinônimo de FORÇA GRAVITACIONAL teremos que admitir que os nossos processos de PESAGEM estão errados. No equador da Terra este erro seria de cerca de 3 partes em 1000 pois o efeito centrífugo no equador é de cerca de 3 cm/s^2 ou de cerca de 0,03 N/kg. Já pela definição da ISO 80000-4 (2006) determinamos o PESO de um corpo no equador multiplicando a sua massa (M) pela aceleração de queda livre local (9,78 m/s^2)  e isto é perfeitamente consistente com os procedimentos usuais de pesagem. A FORÇA GRAVITACIONAL que a Terra exerce sobre este mesmo corpo no equador é maior, valendo cerca de M vezes 9,81 m/s^2.

Vou completar a discussão com o que acontece na Estação Espacial Internacional. No sistema de referência da Estação a aceleração de queda livre é nula, a menos de pequenos efeitos discutidos em MICROGRAVIDADE: Forças de maré na Estação Espacial Internacional? e, portanto, o peso dos objetos neste sistema de referência é nulo; assim sendo, tudo que está na Estação se encontra em estado de imponderabilidade, “flutuando” em microgravidade. Entretanto NÃO é nula a força gravitacional exercida pela Terra em qualquer objeto da Estação pois o campo gravitacional da Terra vale ali cerca de 8,6 N/kg (8,6 m/s^2).

É importante destacar que somente em sistemas de referência inerciais as definições de PESO e FORÇA GRAVITACIONAL são convergentes. Isto porque, enquanto a aceleração de queda livre depende do sistema de referência, a intensidade do campo gravitacional não depende.

Cabe ainda um comentário. É óbvio que para um aluno que está sendo iniciado em Mecânica esta diferença entre PESO e FORÇA GRAVITACIONAL deve ser omitida sob pena de se prejudicar o entendimento do conceito. Afinal, no sistema de referência da Terra a diferença entre o PESO e a FORÇA GRAVITACIONAL é no máximo de três partes em mil.

ADICIONADO em 03/01/2022 – Vide Massa não é peso.

“Docendo discimus.” (Sêneca)

_______________________________________

Comentários no Facebook

Zé Antônio Bocchi – “Há uma definição de PESO como a força que impede que um corpo esteja em queda livre (por exemplo: Weight). Neste caso o PESO seria uma força PARA CIMA, contra a orientação da aceleração de queda livre local.” Qual a natureza desta força? é eletromagnética?

Fernando Lang da Silveira  – Por esta definição a força pode ser, por exemplo, uma força normal à superfície de apoio, uma força elástica em uma mola, uma força tensora em um fio, uma força de empuxo hidrostático em um corpo flutuante, … . Todas estas forças seriam eletromagnéticas. Já pela definição da ISO, admitindo que o peso seja para baixo (pois isto não está claro na definição já que a mesma refere apenas o módulo), o PESO seria a composição de uma força gravitacional com uma força INERCIAL devida à aceleração do sistema de referência.

Visualizações entre 27 de maio de 2013 e novembro de 2017: 9684.