Força exercida pela água ao passar por uma curva em um canal

20 de abril, 2015 às 11:16 | Postado em Cinemática, Mecânica, Mecânica de fluidos

Qual seria aproximadamente a força que uma massa de água corrente, com velocidade 4,5 m/s produzirá no momento que fizer uma curva de 90 graus no canal? O volume de água seria de 36 metros cúbicos a cada segundo.

Quando uma velocidade V constante em módulo muda de orientação por 90 graus, a variação da velocidade é √2 (raiz quadrada de 2) vezes V, ou seja, ΔV=√2.V. A propósito veja Variação da velocidade no MCU?

No caso específico, quando a água que se desloca no canal a 4,5 m/s cumpre a curva que a desvia em 90 graus, a variação da sua velocidade vale aproximadamente ΔV=√2.4,5=6,4 m/s.

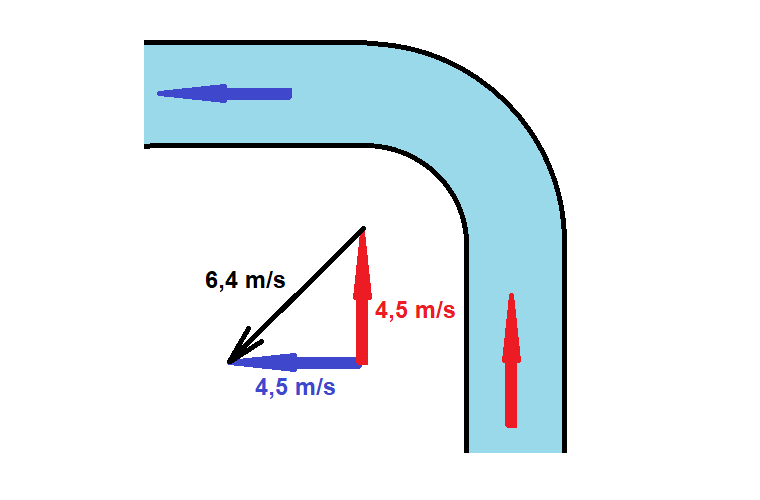
Se a cada segundo tal variação de velocidade acontecer então o valor da aceleração média ao fazer a curva é cerca de 6,4 m/s². A aceleração instantânea ao longo da curva dependerá da forma da trajetória efetivamente cumprida pela água ao cruzar a curva do canal.

Se a cada segundo passar pela curva apenas 1 kg de água, a resultante MÉDIA das forças ao longo da curva sobre esta massa de água, de acordo com a Segunda Lei de Newton, é cerca de 1kg.6,4m/s² = 6,4 N.

Como a vazão no canal é de 36 m³/s tal implica que, dado que a densidade da água é 1000 kg/m³, a cada segundo 36000 kg de água mudam sua velocidade na curva. Então a força resultante média exercida na água na curva é 36000 vezes 6,4 N, ou seja, cerca de 230 mil newtons ou cerca de 23 mil quilogramas-força.

A orientação da resultante das forças que o canal exerce na água que cruza a curva é para dentro da curva e, portanto, a água pressionará o canal para fora da curva.  Adicionalmente existirá um outro efeito, não apenas na curva mas em qualquer região do canal, que consiste em que o canal sofra um força de arrasto viscoso no sentido do movimento da água. Vide Hidrodinâmica em Física Médica.

**- OBSERVAÇÃO IMPORTANTE: A compreensão de que um movimento não retilíneo possui aceleração, mesmo tendo velocidade com módulo ou magnitude constante (ou segundo os defensores da cinemática escalar, a velocidade escalar constante), é prejudicada por esdrúxulas definições de aceleração escalar, e velocidade escalar, deslocamento escalar … . Vide Velocidade média x velocidade escalar média.

COMENTÁRIOS EM UMA COMUNIDADE DE FÍSICA DO WhatsApp em 22/04/2025:

CG – Oi, prezado professor Lang. Eu não entendi o porquê de se afirmar que a variação de velocidade de 6,4 m/s ocorreria a cada segundo. Não precisaria saber o comprimento do tubo ao longo da curva para saber quanto tempo o fluido levaria para realizar a curva completa para poder dizer que a aceleração média seria a variação de velocidade de 6,4 m/s nesse intervalo de tempo?

Penso que, para um mesmo desvio de 90°, se a curvatura do tubo for mais suave (raio maior), o tempo para o fluido completar a curva seria maior de forma que a aceleração média seria menor. Por isso, fiquei em dúvida se não seria necessário conhecer o comprimento do tubo ao longo da curva.

Olhando com atenção, vejo que vc escreveu: “Se a cada segundo tal variação de velocidade acontecer então o valor da aceleração média ao fazer a curva é cerca de 6,4 m/s²”. Provavelmente o “a cada segundo” seja apenas uma suposição.

LANG – Olá CG. O que realmente importa é que neste canal a cada segundo 36.000 kg de água alteram a sua velocidade em 6,4 m/s. Isto implica em uma força média (variação do momento linear da água pelo tempo em que acontece) de 36.000kgX6,4m/s divididos por 1s, resultando em aproximadamente 230.000 newtons. A orientação da força sobre a água aponta para dentro da curva (orientação de delta V na figura) e então a água faz uma força para fora. Não está contabilizado neste raciocínio o arrasto viscoso no encanamento.

CG – O que me surpreende é que assim o raio da curvatura do tubo não importa, importa apenas que o fluido virou 90°. Obrigado pelo seu feedback.

“Docendo discimus.” (Sêneca)

Visualizações entre 27 de maio de 2013 e novembro de 2017: 1304.