Cálculo do torque de tração em um veículo automotor

5 de maio, 2022 às 11:25 | Postado em Atrito, Mecânica, Mecânica de fluidos

Eu vi na postagem Torque necessário para tirar o veículo do repouso o cálculo de torque onde a equação é Τ_traçao= α.M.g.R, onde alfa é o coeficiente de resistência ao rolamento dos pneus, M é a massa do veículo  em kg, g é força da gravidade e R raio da roda em metro. Gostaria de saber a equação acrescentando ângulo de inclinação do plano de rodagem.

Grato

Das equações 7 e 26 do artigo Potência de tração de um veículo automotor que se movimenta com velocidade constante  é obtida a equação para o torque de tração (Τ_traçao) em um veículo automotor:

Τ_traçao ≈ (α.P.cosθ + P.senθ  + ½ρ.C.S.v²).R  ,   (1)

onde α é o coeficiente de resistência ao rolamento dos pneus, P é o peso do veículo, θ é o ângulo de inclinação da pista de rolamento, ρ é densidade do ar, C é o coeficiente de resistência aerodinâmica do veículo, S é a área frontal do veículo, v é o valor da velocidade do veículo em relação ao ar e R é o raio da roda do veículo.

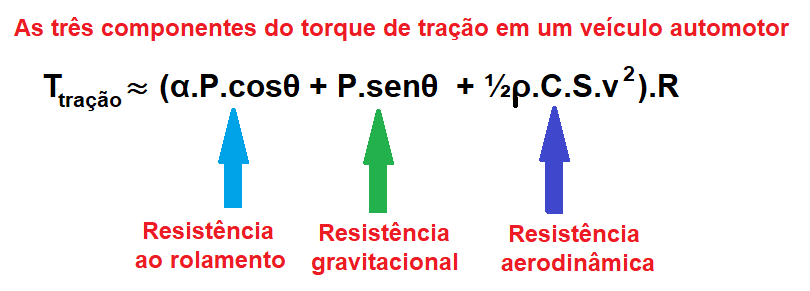
A equação 1 se reduz a Τ_traçao ≈ α.P.R quando a pista não é inclinada e o termo que envolve a velocidade (a resistência oferecida pelo ar) é desprezível, isto é, para pequenas velocidades do veículo prepondera a resistência ao rolamento. Vide a discussão no final da secção 5 do artigo Potência de tração …. Na secção 7 do artigo as rampas são levadas em consideração.

Finalmente, dado que o coeficiente de resistência ao rolamento de pneus sobre o asfalto é aproximadamente 0,01, e como nas rodovias BRs a inclinação máxima é cerca de 3° (vide Por que a inclinação máxima nas BRs não deve exceder 3 graus?), a resistência gravitacional em aclives com tal inclinação exige um torque de tração P.senθ.R  (conforme a equação 1), resultando ser este torque 5 vezes maior do que o torque de tração α.P.R necessário para superar a resistência ao rolamento.

“Docendo discimus.” (Sêneca)