Reconstituição de acidentes de trânsito: um exemplo.

19 de abril, 2021 às 18:49 | Postado em Mecânica, Outros temas

Saudações mestre. Fiquei curioso para saber como os peritos efetuam os cálculos que determinam a velocidade que um veículo possuía antes de uma colisão, tendo como dados as marcas de frenagem numa pista asfaltada e a deformação do veículo na colisão.

Pode dar um exemplo hipotético?

As metodologias para a reconstituição de acidentes utilizados por peritos criminais, geralmente com formação em cursos de Engenharia Mecânica ou Física, são diversos.

Utilizam-se, principalmente, o Teorema de Conservação da Quantidade de Movimento Linear (TCQML) para determinação de velocidades logo antes e logo após os impactos e o Teorema Trabalho-Energia Mecânica (TTEM), que relaciona o Trabalho de forças, como a de atrito cinético entre os pneus e a pista, com a Energia Cinética do móvel para a estimativa das velocidades nos instantes de início de frenagem, a partir das marcas deixadas na pista.

Não se utiliza a lei de Conservação da Energia Mecânica nas colisões pelo motivo dela não se conservar em colisões inelásticas, pois a Energia Mecânica se transforma em outras formas de energia quando os objetos que colidem ficam deformados permanentemente, por exemplo.

Existe uma grande dificuldade em se desenvolver métodos que utilizam a quantidade de deformação dos veículos para se determinar as velocidades de colisões, pois os automóveis são feitos de diferentes materiais com diferentes coeficientes de deformação e de rigidez. Mesmo assim, existem alguns modelos que funcionam satisfatoriamente bem em alguns casos específicos.

Em acidentes com colisão em postes de concreto, utiliza-se um modelo para a estimativa da velocidade na colisão a partir do grau de destruição e do deslocamento do poste, a partir de informações dos testes de avaliação de resistência e qualidade que são feitos antes de serem instalados. Em alguns casos de atropelamento, utiliza-se a mesma ideia para estimar velocidades a partir do tipo e do grau de destruição do vidro do para-brisa.

Entretanto, recentemente, estão sendo utilizados métodos computacionais de simulação, como os programas Virtual Crash Accident Reconstruction (disponível em https://www.vcrashusa.com/home#home-vc) e o PC-Crash (disponível em http://www.pc-crash.com/), que possibilitam a entrada de diversos dados periciais do local, dos veículos e objetos envolvidos, resultando em uma modelagem computacional de reconstituição muito fiel aos acontecimentos.

Os dados periciais são obtidos a partir do uso de diversas ferramentas, como o escaneamento a Laser do local, utilização de imagens via satélite e por drones, filmagens obtidas por câmeras de segurança e por câmeras instaladas nos próprios veículos envolvidos, registros de dados por aparelhos de GPS e por módulos de controle de airbags ou CDRs (Crash Data Recorders), semelhantes às “caixas pretas” em aviões, além do uso de microscopia para análise de peças. Isso tudo somado às técnicas tradicionais de medidas com fitas métricas, esboços e desenhos técnicos, fotografias do local, medidas diretas de coeficientes e fatores de atrito, etc.

Quando não se conseguem obter dados suficientes a partir dos vestígios encontrados após os acidentes, utilizam-se métodos numéricos e se estimam faixas de valores de velocidades, onde já se consegue perceber se um veículo estava ou não em alta velocidade, já ajudando no julgamento dos casos pela justiça.

Então, vou propor um exemplo onde podemos, a partir de dados que podem ser obtidos com as técnicas citadas, aplicar as ferramentas físicas do TCQML e do TTEM para as estimativas de valores de velocidades para um caso de um abalroamento de um automóvel com um animal.

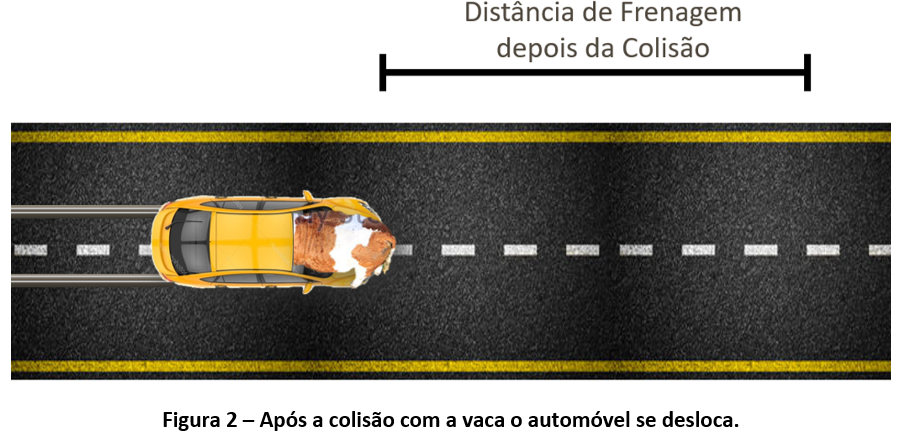
Exemplo: Numa rodovia reta, plana e horizontal, pavimentada com asfalto, um automóvel colidiu com sua dianteira contra uma vaca que estava parada no meio da via (Figura 1). Na colisão, o animal acaba quebrando o para-brisas e ficando preso ao veículo, sendo levado por uma distância de 20,0m até a parada do veículo. Antes do impacto, o carro já vinha usando os freios, deixando marcados 6,2m de frenagem, antes de colidir.

Quais são os valores estimados da velocidade do automóvel e da distância entre ele e a vaca no instante em que o condutor a avistou?

Dados obtidos a partir da análise pericial do local após o ocorrido:

Massa do automóvel: M = 2000kg.

Massa da vaca: m = 1000kg.

Aceleração da gravidade: g = 10m/s².

Distância de frenagem antes da colisão: 6,2m.

Distância de frenagem após a colisão até a parada do conjunto: 20,0m.

Considerar que o tempo de pré-frenagem foi de 1,5s.

Coeficiente de atrito cinético entre pneu e asfalto seco µ = 1,0.

Desconsiderar qualquer tipo de efeito ou impedimento realizado pelo ar.

Supor a colisão perfeitamente inelástica e que o veículo se move com velocidade constante durante o tempo de reação.

1º) Calcular a velocidade do conjunto logo após a colisão a partir da distância de frenagem depois da colisão.

A partir do Teorema Trabalho-Energia Mecânica relacionamos o trabalho das forças não conservativas com a variação da energia mecânica:

Ao se desprezar os efeitos do ar, temos que a Energia Cinética associada ao conjunto será transformada em outras formas de energia através do trabalho da força de atrito cinético até a parada completa do sistema carro e vaca.

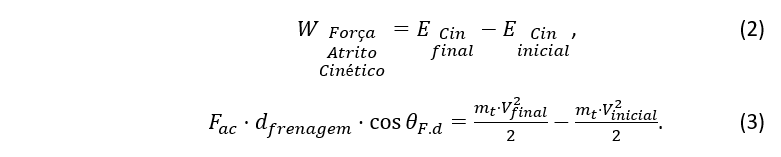
A força de atrito é dada pelo produto do coeficiente de atrito e a força normal que, neste caso, tem módulo igual ao peso do conjunto. Além disso, a força de atrito tem sentido oposto ao deslocamento de frenagem do sistema, que para após 20m. Então

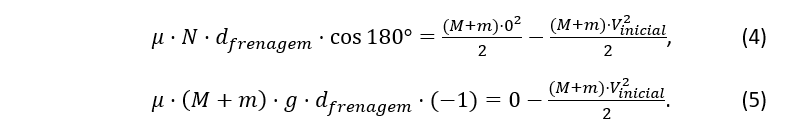
A velocidade inicial indicada na equação 5 é, na verdade, a velocidade logo após a colisão. Desta forma

Ao se substituir os valores na equação 9, temos que

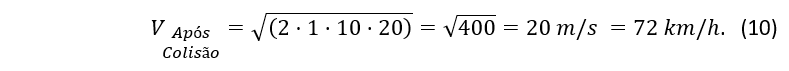
2º) Calcular a velocidade do veículo logo antes da colisão, considerando-a como totalmente inelástica.

Para isso, usamos o Teorema da Conservação da Quantidade de Movimento Linear:

Como a vaca estava inicialmente em repouso, a velocidade dela logo antes da colisão é nula. Após a colisão, a velocidade da vaca é a mesma do veículo, pois eles ficam acoplados na colisão totalmente inelástica.

Como M=2000kg , m=1000kg    e  V_Após=20m/s obtém-se

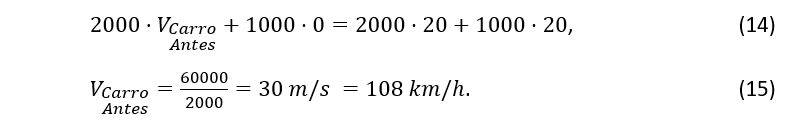
3º) Calcular a velocidade do veículo no início da frenagem.

Aqui, podemos utilizar o mesmo raciocínio do primeiro passo. Assim a partir do Teorema Trabalho-Energia Mecânica, podemos escrever que

4º) Calcular a distância até a vaca quando foi avistada pelo condutor.

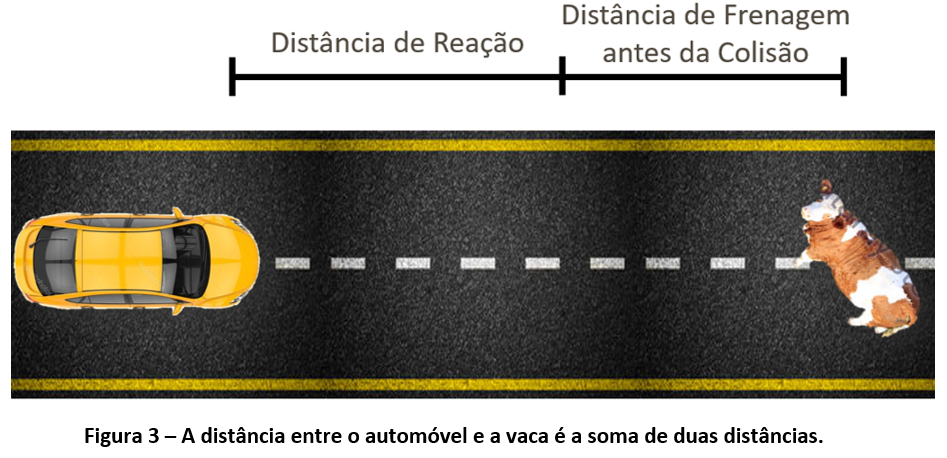
Conforme representado na Figura 3 a distância entre o automóvel e a vaca no momento em que o motorista a percebe é a soma de duas distâncias.

Como durante a distância de reação o veículo trafegou com velocidade constante, a distância percorrida neste intervalo é calculada a partir da relação abaixo:

 Portanto, quando a vaca foi avistada, ela estava a pouco mais de 50m à frente do veículo, que trafegava com velocidade certamente superior a 100 km/h.

Outras postagens sobre o tema: Acidente de trânsito.

Nota adicional: Com o  intuito de contribuir para o ensino de Física e para a formação de pessoas educadas e prudentes no trânsito, a partir da cooperação e disseminação de conhecimentos técnicos científicos por professores e possíveis colaboradores, disponibiliza-se um produto educacional, na forma de repositório digital, contendo os roteiros das aulas, guias de atividades, materiais e artigos extras para aprofundamento, além de sugestões de vídeos e slides, para livre reprodução, adaptação e aplicação. Vide Física e educação para o trânsito.