Duas retas dos Mínimos Quadrados no mesmo conjunto de pontos?
5 de agosto, 2022 às 20:16 | Postado em Estatística e probabilidade, incertezas experimentais, Matemática
Respondido por: Prof. Fernando Lang da Silveira - IF-UFRGSCaro Professor,
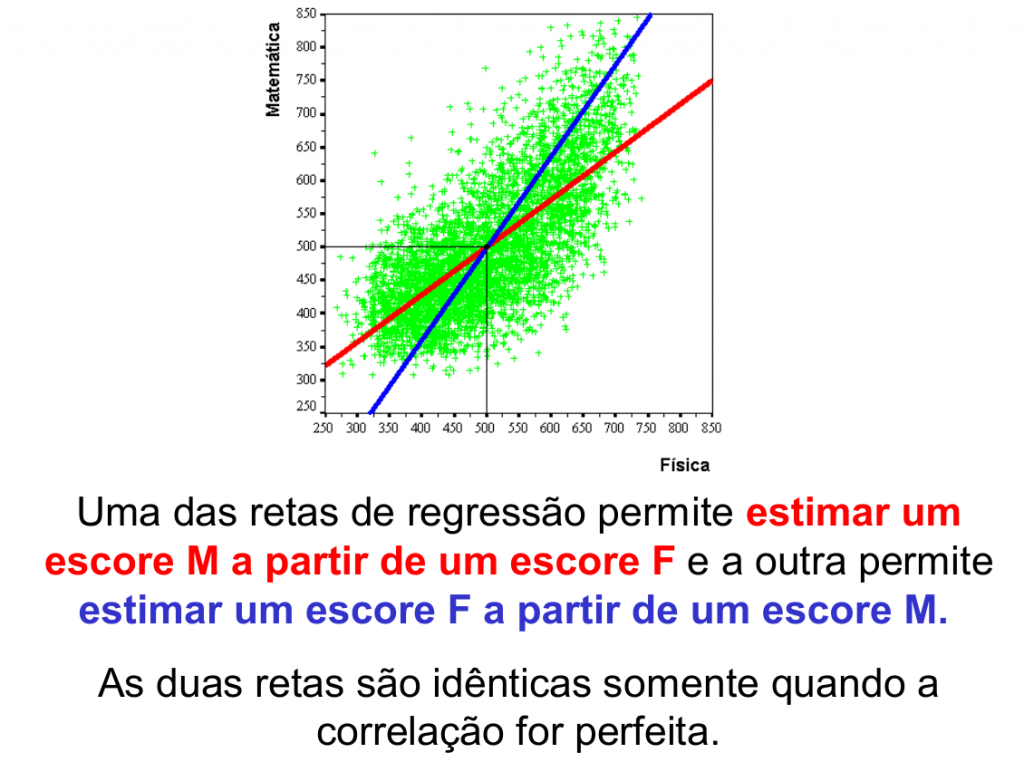
eu estava olhando a apresentação chamada “Métodos quantitativos aplicados à pesquisa em ensino – Seminário 3“. Os primeiros slides são muito informativos! Mas eu queria falar do slide 22 Nele é mostrado que existe uma assimetria da regressão linear frente a escolha da variável “independente”. Parece que devo deduzir disso que a regressão linear é portanto uma metodologia imprópria para informar a respeito de relações matemáticas entre as duas variáveis? Deveria ser encontrar uma função tendo como requisito mínimo uma invariância frente a troca das “funções” das duas variáveis envolvidas. Será que tem algo elementar que eu não entendi?
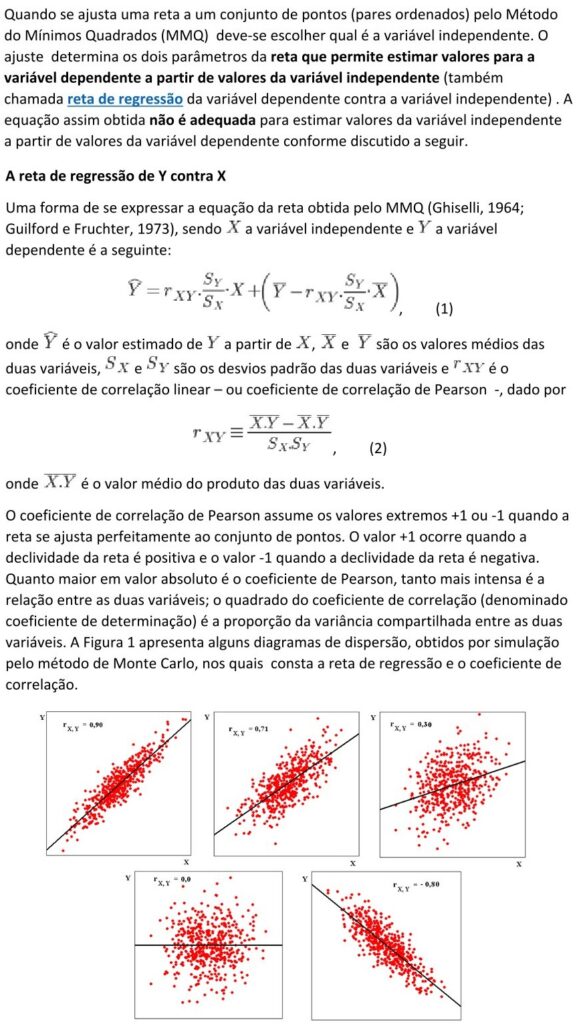
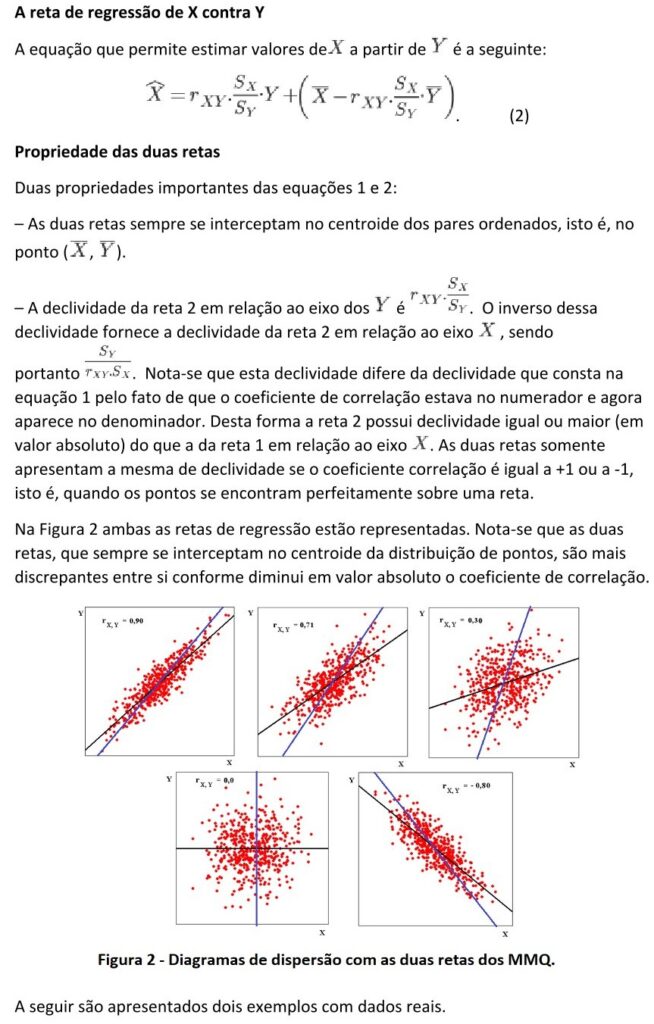
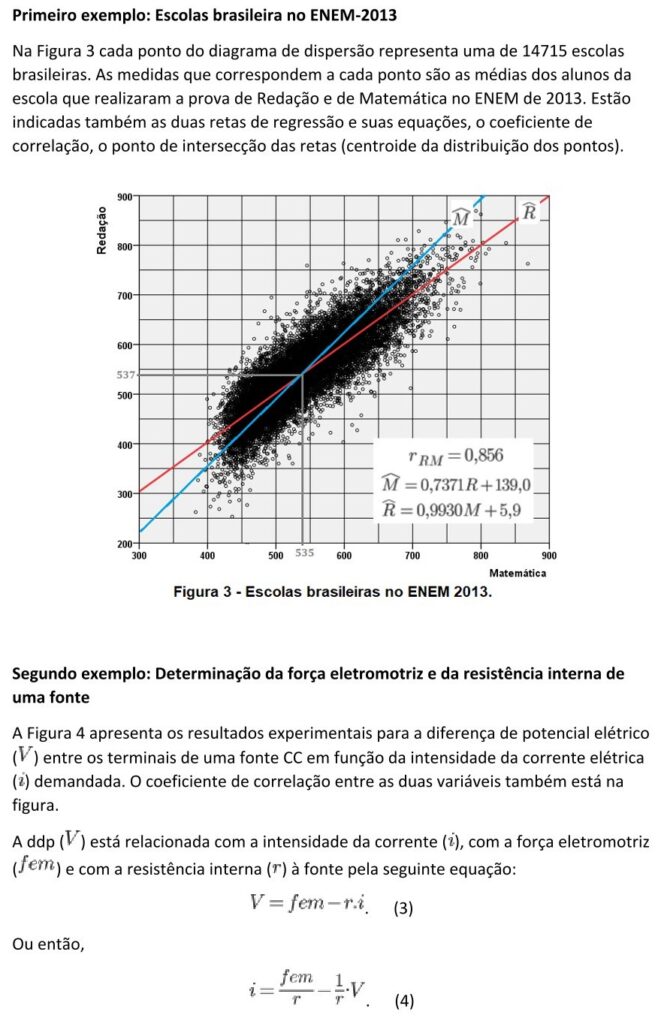
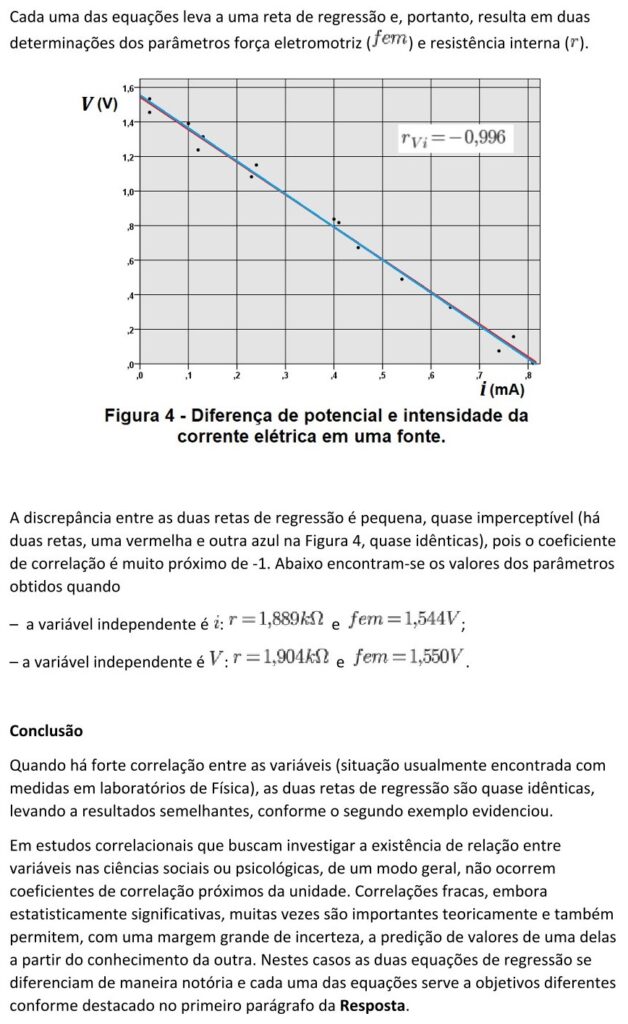
REFERÊNCIAS.
Ghiselli, E. E. Theory of psychological measurement. Tata MeGraw-Hill, Bombay, 1964.
Guilford, J. P. E Fruchter, B. Fundamental statistics in psychology and education. McGraw-Hill, New York, 1973.
OBSERVAÇÃO: como este questionamento foi feito no Research Gate, lá também se encontra esta resposta em documento pdf. Vide Duas retas dos Mínimos Quadrados no mesmo conjunto de pontos?
Comentários aditados em 09/08/2022:
– O coeficiente de correlação de Pearson é invariante frente a troca de uma variável pela outra, assim como também é invariante frente a mudanças de escala em qualquer uma das variáveis. Ele é a declividade da reta de regressão de Y contra X ou de X contra Y quando as variáveis estão padronizadas, isto é, possuem médias nulas e variâncias unitárias.
– Sobre relação de causalidade. Mesmo quando a correlação é extremamente forte, a relação de causalidade não está garantida. A correlação ou variação concomitante entre duas variáveis é apenas uma das três condições para se estabelecer uma relação causal. As outras duas são: a prova da relação temporal (efeito não antecede a causa no tempo); a prova da exclusão de outras variáveis explicando a variação concomitante.
– Quando teoricamente é esperada uma correlação perfeita entre duas variáveis (por exemplo, no caso da relação entre temperatura e volume em um gás ideal sob pressão constante), as medidas dessas duas variáveis em laboratório não resultarão em um coeficiente de correlação igual +1 por causa dos erros de medida. A propósito veja Sobre a determinação do zero absoluto.
“Docendo discimus.” (Sêneca)

Professor, A Análise de Regressão não tem por objetivo estabelecer uma Relação de Causa e Efeito. E no cálculo do Coeficiente Correlação podemos ver que tanto faz falar Y está ou não relacionada com X ou falar X está ou não relacionada a Y. Isto pode ver visto na Tabela do Cálculo do Coeficiente de Relação de Pearson onde podemos trocar as duas Colunas de Y e de X que o Resultado numérico do Coeficiente de Correlação de Pearson é o mesmo. É claro que se um fenômeno Físico tipo X=Temperatura e y=Pressão vai mostra uma relação Forte ou seja Coeficiente de Correlação exatamente igual a 1 (Relação extremamente Forte), pois neste caso a Correção entre X e Y (ou entre X e Y) já é uma Correlação de Causa e Efeito. A Curva de Regressão é a que estudamos em Física na parte de Termodinâmica uma Equação mostrando que quando A Temperatura aumenta a Pressão aumenta também.
– O coeficiente de correlação de Pearson é invariante frente a troca de uma variável pela outra, assim como também é invariante frente a mudanças de escala em qualquer uma das variáveis. Ele é a declividade da reta de regressão de Y contra X ou de X contra Y quando as variáveis estão padronizadas, isto é, possuem médias nulas e variâncias unitárias.
– Mesmo quando a correlação é extremamente forte, a relação de causalidade não está garantida. A correlação ou variação concomitante entre duas variáveis é apenas uma das três condições para se estabelecer uma relação causal. As outras duas são: a prova da relação temporal (efeito não antece a causa no tempo); a prova da exclusão de outras variáveis explicando a variação concomitante.
– Mesmo quando esperamos teoricamente que a correlação entre duas variáveis seja perfeita (por exemplo, no caso da relação entre temperatura e volume em um gás ideal sob pressão constante), as medidas dessas duas variáveis em laboratório não resultarão em um coeficiente de correlação igual +1 por causa dos erros de medida. A propósito veja Sobre a determinação do zero absoluto.
