Por que equação de regressão?

14 de setembro, 2022 às 16:59 | Postado em Estatística e probabilidade, incertezas experimentais, História da Ciência, Matemática

Professor Lang

Uma questão de terminologia que tenho diz respeito à sua postagem Duas retas dos Mínimos Quadrados no mesmo conjunto de pontos?:

Qual a razão de se denominar a equação de ajuste pelo método dos mínimos quadrados de equação de regressão? Qual é a origem do termo regressão neste contexto?

Os textos de estatística que consultei usam essa terminologia sem justificativa. O senhor poderia elucidar esta questão? Agradeço antecipadamente.

I.- Galton e a regressão para a média

A terminologia equação de regressão para o ajuste de uma curva a um conjunto de pontos ou pares ordenados remonta ao inglês vitoriano Francis Galton (1822-1911), notável polímata (estatístico, sociólogo, psicólogo, antropólogo, geógrafo, inventor), em seu artigo de 1886 Regression Towards Mediocrity in Hereditary Stature.

Neste artigo Galton relata o efeito de regressão para a média na hereditariedade da estatura dos pais e filhos. Ao investigar a estatura de pais e filhos em uma amostra de ingleses encontrou que “pais altos tem filhos altos, entretanto os filhos são em média mais baixos do que os pais” e que “pais baixos tem filhos baixos, entretanto os filhos são em média mais altos do que os pais”. Ou seja, a estatura média dos filhos em estratos de pais afastados da média do grupo completo regride em direção esta média (se aproxima desta média).

Como os dados de Galton estão disponíveis (vide Dados de Galton), apresenta-se a seguir uma nova análise para caracterizar o efeito de regressão para a média.

A Figura 1 representa no eixo das abcissas a estatura média dos pais (estatura parental) e no eixo das ordenadas a estatura do filho(a). Como existe uma diferença de estatura entre homens e mulheres, Galton corrigiu a estatura das mulheres para equivaler a dos homens. Esta correção foi feita multiplicando a estatura das mulheres por 1,08. A estatura média dos pais (estatura parental) é uma média aritmética da estatura do pai com a estatura corrigida da mãe.

A média de todas as estaturas parentais (são 896 pontos no diagrama de dispersão da Figura 1) é 175,8cm e a média de todas as estaturas dos filhos também vale 175,8cm. Em verde está o centroide C(175,8cm, 175,8cm) da distribuição dos pontos cujas coordenadas são as respectivas médias das 896 estaturas parentais e dos filhos.

Como se observa neste conjunto de dados, em média a estatura parental é igual à estatura dos filhos.

II.- Regressão da estatura dos filhos em direção à média das estaturas parentais

A seguir estudaremos como as estaturas parentais e dos filhos se apresentam em estratos dos 896 pares ordenados que constituem as medidas de Galton em 1886.

Adotaremos um critério de estratificação das estaturas parentais, as ordenando em ordem crescente, e tomando grupos sucessivos que perfazem 10% das 896 estaturas parentais. Ou seja, 10% das estaturas parentais a começar pelos menores valores constituem o primeiro estrato. A seguir, no segundo estrato, comparecem mais 10% das estaturas parentais em ordem crescente e assim por diante. As estaturas parentais são agrupadas então em 10 estratos.

Depois calculam-se as médias das estaturas parentais e dos filhos em cada um dos estratos. Esses resultados (10 pontos cujas coordenadas são as médias das estaturas nos estratos) estão representados no diagrama de dispersão da Figura 2 e também está indicada a reta que configuraria que em média as estaturas parentais e dos respectivos filho seriam iguais.

Conforme se observa na Figura 2, quanto mais distante estão os pontos vermelhos do centroide C, tanto mais discrepante é a média da estatura dos filhos em relação à média da respectiva estatura parental. Os pontos vermelhos se encontram abaixo da reta azul (F=P) à direita do centroide e acima à esquerda do centroide.

Uma análise semelhante a esta em 1886 levou Galton a concluir que “pais altos tem filhos altos mas em média mais baixos do que os pais” e “pais baixos tem filhos baixos mas em média mais altos do que os pais”. Ou seja, quanto mais extremas são as estaturas parentais, tanto maior é a regressão da média da estatura dos filhos em direção à média de todos os pais ou filhos. Por exemplo, o estrato com os pais mais altos possui estatura média de 184,4cm e seus filhos de 182,4cm, apresentando então uma regressão de 2cm em direção à média de todo o grupo de pais ou filhos (175,8cm). No outro extremo, os pais mais baixos apresentam estatura média de 167,5cm enquanto seus filhos possuem a estatura média de 170,4cm, regredindo a estatura dos filhos 3cm em direção à média do grupo total (175,8cm).

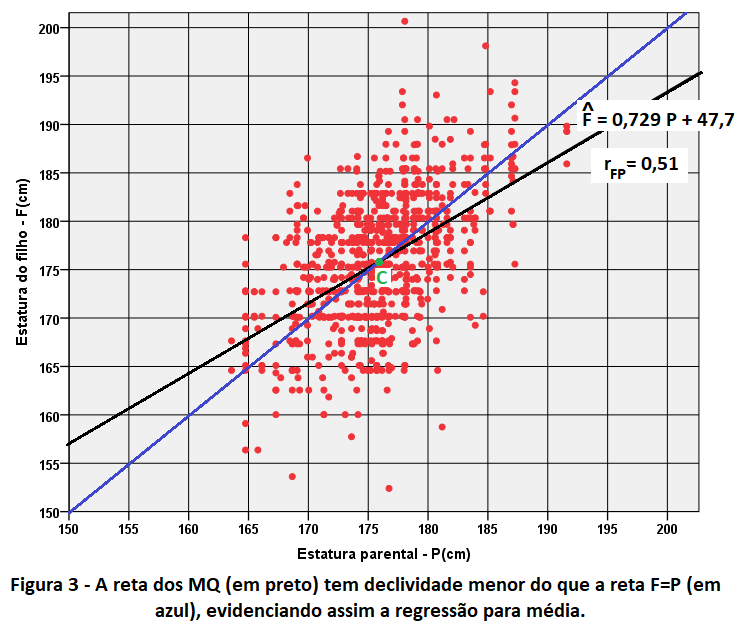
A equação da reta dos Mínimos Quadrados (MQ) ajustada aos pontos da Figura 1, tendo como variável dependente a estatura do filho (F), também descreve a regressão para média como se nota na Figura 3. A reta dos MQ está na cor preta e a reta que indica a mesma estatura para pais e filhos tem cor azul. Na figura também está indicado o coeficiente de correlação de Pearson entre F e P (r_FP) e a equação da reta ajustada pelo método do MQ ou simplesmente reta de regressão (vide mais sobre a reta em Duas retas dos Mínimos Quadrados no mesmo conjunto de pontos?).

III. – É a regressão para média nas estaturas de pais e filhos uma lei biológica?

Quando duas variáveis não apresentam correlação perfeita, a regressão para média acontecerá em grupos ou estratos definidos por seus valores distantes da média do grupo íntegro (média total) e é tanto maior quanto mais afastado da média total se encontra o estrato. Ou seja, a regressão para a média é uma “lei estatística”, decorrente das flutuações naturais das variáveis não perfeitamente correlacionadas, levando a ter nesses estratos casos que não repetirão na outra variável desvios absolutos em relação à média tão grandes.

A regressão para média no estudo de Galton também ocorre quando se toma como referência para definir os estratos a estatura dos filhos. Ela igualmente pode ser observada quando se ajusta a reta dos MQ tomando como variável independente a estatura dos filhos e como variável dependente a estatura parental. O gráfico da Figura 4 evidencia as regressões para a média nas duas retas dos MQ indicadas em cor preta ao se constatar que ambas as retas possuem declividades em relação ao eixo da variável independente menor do que a da reta azul (as duas declividades, conforme se observa na Figura 4, são menores do que um, valendo 0,729 e 0,357).

Incorre-se na falácia de Galton quando se interpreta a regressão para a média como decorrência de algum suposto efeito causal relacionado ao contexto no qual as duas variáveis pertencem. Neste estudo de Galton (e em outros também, por exemplo no seu estudo sobre o tamanho de sementes) incorre-se na falácia de Galton quando se atribui a regressão para a média como consequente da biologia dos humanos (ou das sementes). É importante adicionalmente observar que as duas retas dos MQ implicam um aparente paradoxo pois não apenas pais altos (baixos) tem filhos altos (baixos), entretanto os filhos são em média mais baixos (altos) que os pais com também filhos altos (baixos) tem pais altos (baixos), entretanto os pais são em média mais baixos (altos) que os filhos.

IV. – Conclusão

Como foi demonstrado, as duas equações da reta dos MQ implicam em regressão para a média. Por essa razão foram denominadas equações de regressão.

Depois a terminologia foi generalizada para qualquer equação ajustada a um conjunto de pontos, inclusive com mais de uma variável independente e também variáveis categóricas, por exemplo regressão múltipla. O termo análise de regressão incorpora uma gama enorme de métodos conforme se verifica em textos de estatística, em materiais na internet e em pacotes estatísticos. Ou seja, o termo regressão teve seu significado enormemente expandido de tal forma que hoje transcende em muito aquilo que Galton em 1886 denominou de regressão para a média.

___________________________________________

Este texto está disponível no Research Gate.

“Docendo discimus.” (Sêneca)