Ajuste de curvas: OLS versus WLS

21 de junho, 2023 às 13:35 | Postado em Estatística e probabilidade, incertezas experimentais, Matemática

Construímos uma tabela com mais de uma centena de pontos experimentais, os quais foram obtidos atribuindo-se 8 (oito) valores distintos a uma variável independente “x”, sendo que, para cada um destes valores, realizamos cerca de 20 repetições do mesmo experimento, e medimos o valor de uma variável dependente “y”.

Conhecida a expressão analítica “y = f(x)” prevista pela teoria, a respeito do comportamento de “y” em função de “x”, a qual envolve parâmetros a serem determinados a partir destes dados experimentais, pretendemos utilizar o método dos mínimos quadrados para obter a curva que melhor se ajusta a estes pontos. A pergunta é: neste método, a soma dos quadrados das diferenças que iremos minimizar deverá ter mais de uma centena de termos, ou podemos trabalhar com a soma dos quadrados de apenas 8 diferenças, a saber, aquelas obtidas considerando, para cada valor de “x”, a média aritmética dos valores de “y” correspondentes fornecidos pelo experimento?

O ajuste de curvas (ou, no jargão dos estatísticos, a determinação da equação de regressão) pelo Método dos Mínimos Quadrados Ordinário (OLS – Ordinary Least Squares) tem como pressuposto (entre outros!) a homocedatiscidade, isto é, a igualdade das variâncias da variável dependente para todos os valores da variável independente. Escrevendo com outras palavras, a dispersão da variável dependente é a mesma para os diversos valores da variável independente. Na figura 1 são apresentados dois conjuntos pares ordenados (x, y), obtidos por simulação usando o método de Monte Carlo, nos quais a variável dependente ora apresenta homocedasticidade, ora heterocedasticidade.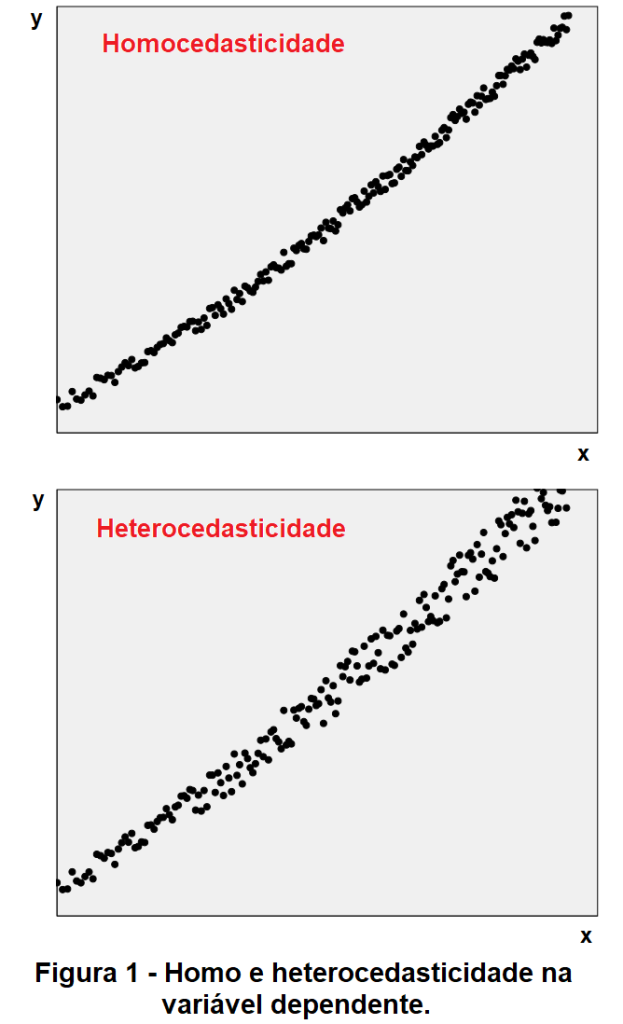

Em caso de heterocedasticidade, o Método dos Mínimos Quadrados Ponderado (WLS -Weighted Least Squares) é a alternativa adequada ao ajuste de uma curva em um conjunto de dados experimentais.

O OLS minimiza o somatório do quadrado dos resíduos. O resíduo é a diferença entre o valor de Y observado e o valor de Y dado pela função de ajustamento escolhida. A minimização do somatório leva a determinação dos valores dos parâmetros da função de ajustamento.

O WLS minimiza o somatório do quadrado dos resíduos ponderados. O peso aplicado a cada resíduo ao quadrado é o inverso da variância de Y calculada para cada particular valor da variável independente. O resíduo neste caso é a diferença entre a média de Y e o valor de Y dado pela função de ajustamento. Desta forma o WLS atribuiu aos pares ordenados (X, Y_médio) pesos diferentes enquanto o OLS opera com pesos idênticos para todos os pontos experimentais.

Um exemplo ilustrativo é apresentado a seguir.

Utilizando o método de Monte Carlo foi simulado um conjunto de pares ordenados com 160 “resultados experimentais”. A variável independente X apresenta valores inteiros no intervalo fechado de 1 até 8. A variável dependente Y  assume valores dados por

Y = -2.X² + 20.X + ϵ ,

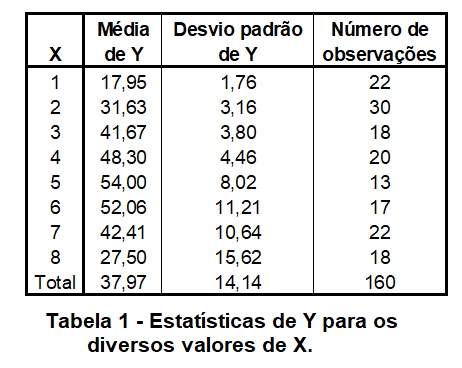
onde ϵ é uma variável aleatória com distribuição uniforme, média zero e variância dependente de X, portanto Y apresenta heterocedasticidade. Os 180 pares ordenados resultantes da simulação se encontram no documento resul_simul.pdf. O número de pares ordenados para cada um dos oito valores de X não é mesmo como pode ser verificado na tabela 1.

Como os “resultados experimentais”  apresentam heterocedasticidade o ajuste da função Y = -b.X² + a.X deve ser conduzido através do Método dos Mínimos Quadrados Ponderados (WLS). Para tanto são calculadas a média e o desvio padrão de Y para cada valor de X, encontrando-se os resultados constantes da tabela 1.

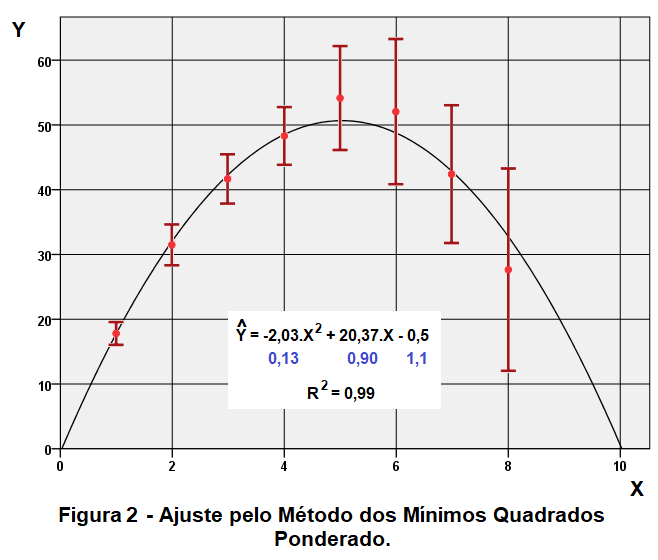
O gráfico da figura 2 apresenta os oito pares ordenados (X, Y_médio), as barras de erro com um desvio padrão de Y, a função “Y chapéu” com os seus três parâmetros obtidos pela aplicação do Método dos Mínimos Quadrados Ponderado (realizado com o pacote estatístico SPSS), o coeficiente de determinação R², e em azul os respectivos desvios padrão (incertezas) dos parâmetros.

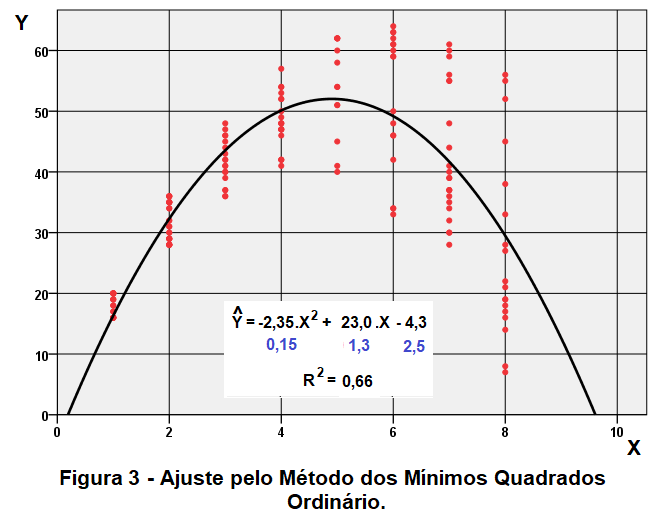
A figura 3, para fins de comparação com o método anterior, apresenta a análise pelo Método dos Mínimos Quadrados Ordinário (OLS). Este procedimento é conduzido com todos os 180 pares ordenados (X,Y) indicados como pontos vermelhos no gráfico.

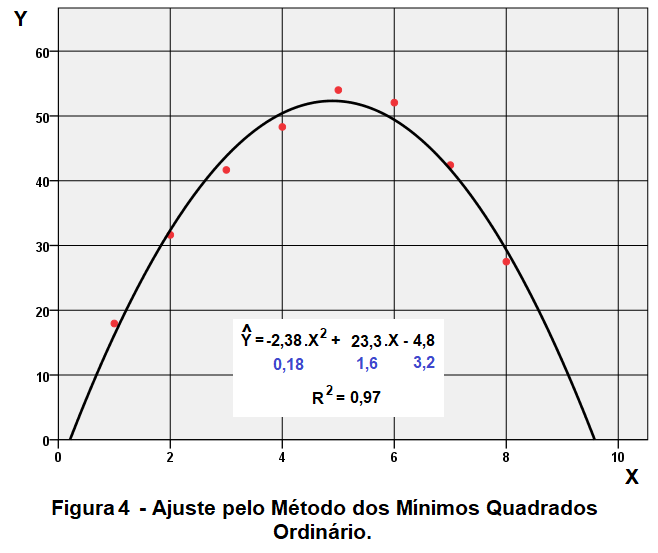
O gráfico da figura 4 apresenta uma última análise pelo Método dos Mínimos Quadrados Ordinário com os oito pares ordenados (X, Y_médio). Nesta análise, diferentemente da primeira, os oito pontos pesam igualmente de acordo com o pressuposto de homocedasticidade que neste caso e no anterior está violado.

CONCLUSÃO

As três análises levam a resultados diferentes, embora semelhantes. É importante notar que o Método dos Mínimos Quadrados Ponderado leva a parâmetros com menores incertezas e maior bondade no ajuste (coeficiente de determinação R² maior) que as outras duas análises utilizando o Método dos Mínimos Quadrados Ordinário. Como neste caso a “verdadeira” função subjacente aos dados simulados é conhecida (Y = -2.X² + 20.X), verifica-se  que a primeira análise leva a parâmetros mais próximos dos “verdadeiros” parâmetros do que as duas outras.

Assim sendo, recomendo utilizar o Método dos Mínimos Quadrados Ponderados no caso concreto do estudo que a perguntante refere.

OBSERVAÇÃO. No Research Gate está disponível este questionamento e a sua resposta em um documento pdf no seguinte endereço: https://www.researchgate.net/publication/371852472

“Docendo discimus.” (Sêneca)