Teste rápido para reconhecer pilha carregada ou descarregada? É fake?

13 de março, 2014 às 21:06 | Postado em Eletricidade

Caro Fernando

Tem algum fundamento no teste que se vê no vídeo How To Test a AA battery, Easiest Way For Any Battery Fast em https://www.youtube.com/watch?v=Y_m6p99l6ME .

Abraços

Quando vi pela primeira vez o vídeo, entendi mal sobre o teste. Entendi que o relevante do teste era se a bateria ficava ou não de pé. Na verdade o que interessa no teste é se ela, ao colidir com o piso duro, repica diversas vezes ou (quase) não repica.

Como havia mal compreendido o teste, induzido pelo que está dito no vídeo indicado, resolvi verificar se de fato uma bateria nova ficava em pé e uma gasta caia de lado após colidir com o piso. Os experimentos que realizei então (março de 2014) me levaram a concluir que uma pilha nova e uma pilha gasta não apresentavam diferença estatisticamente significativa no comportamento de ficar de pé ou deitada depois de cair sobre o piso duro.

Semanas depois observei que diversas pilhas gastas, que estavam estocadas muito tempo em minha casa esperando o descarte, tinham a placa do fundo (polo negativo) separada do corpo da pilha. Todas as outras pilhas do estoque estavam com com esta placa abaulada para fora, como se a pressão interna à pilha tivesse aumentado, estufando o fundo da pilha.

Daí me dei conta que no teste o importante era observar os múltiplos repiques da pilha gasta ao colidir com o piso duro. Quando refiz a testagem com estas pilhas gastas, comparando com o comportamento de repique de pilhas novas, obervei que DE FATO as pilhas usadas repicavam mais do que as velhas.

Esqueci de alterar a postagem antiga aqui no CREF e somente hoje (22 de janeiro de 2015), graças a uma amiga ter novamente me indicado um material sobre o efeito, é que refiz esta postagem. A antiga postagem se encontra abaixo, agora em vermelho, como curiosidade do teste que fiz em março de 2014. Mantenho a antiga postagem também por um relato sobre o que um aluno da engenharia nos anos 80 verbalizou a propósito de baterias de chumbo ácido.

Conclusão: De fato com diversas pilhas usadas verifiquei que repicam mais vezes sobre o piso duro do que as pilhas novas.

Resta ainda esclarecer porque as pilhas usadas apresentam o estufamento da placa junto ao polo negativo!

OBSERVAÇÃO: Neste vídeo –  http://youtu.be/qrGV7zKEdtU   -, indicado pelo Felipe B. Ben há uma explicaçãopara o maior coeficiente de restituição apresentado pelas usadas em relação às novas.

_______________________________________________________________

ANTIGA POSTAGEM (feita em 13/03/2013) COM OS EXPERIMENTOS QUE ENTÃO REALIZEI

Quando uma fonte eletroquímica “descarrega” (diminui a sua energia química) ocorrem reações químicas no seu interior que podem modificar a distribuição de massa e a própria massa da fonte quando houver produção de gases e vapores e estes  escaparem da fonte.

Há muitos anos em uma aula para as engenharias, quando discutia sobre fontes eletroquímicas, um aluno assim se manifestou: “Quando a bateria ganha carga ela fica mais pesada!“. Os demais alunos acharam graça!

Um dos alunos até concordou mas complementou dizendo que o ganho de massa ganha seria desprezível frente a massa total da bateria. Continuou argumentando que a bateria ganharia elétrons no processo de carga mas que, como era bem sabido, a massa dos elétrons é desprezível frente à massa do restante dos átomos e moléculas.

Eu então lhe disse que de fato a bateria NÃO ganhava elétrons no processo de carga pois para carregá-la se faz circular uma corrente, isto é, se coloca por um dos bornes da bateria elétrons e se tira pelo outro a mesma quantidade de elétrons e que, portanto, a carga total da bateria permanecia inalterada durante o processo de “carga”. Idem para a “descarga”.

Assim sendo “carregar” uma bateria é uma forma alternativa a corretamente se dizer energizar a bateria, estocar ENERGIA QUÍMICA na bateria.

O aluno que havia se manifestado inicialmente retornou insistindo: “O meu pai que é eletrotécnico mede as mudanças de massa para saber que a bateria está ou não carregada.“

Quando ele disse isso me “caiu a ficha”! O pai do aluno de fato media a DENSIDADE do eletrólito em baterias chumbo-ácido pois esta aumenta em um pouco mais de 5% durante o processo de “carga”. Este aumento permite saber o estado da “carga” da bateria.

Agora vou analisar a mensagem que o vídeo pretende passar. 

Considerei a priori que o vídeo  é uma grande empulhação pois, se deixarmos deixar cair um objeto com a forma de uma pilha conforme se vê na demonstração, é mais provável que o objeto termine deitado de lado. A base sendo muito estreita comparada com a altura da pilha, leva a que a posição de pé seja pouco estável, sendo portanto improvável de qualquer forma o resultado mostrado. Mesmo assim considerando resolvi fazer um experimento com uma pilha “morta” e uma pilha “nova” de mesma marca.

Como estava em casa não tinha os recursos de um laboratório de Física mas testei se o centro de gravidade de ambas as pilhas se localizavam aproximadamente no mesmo local da pilha. Equilibrei ambas de lado sobre a base mais estreita que tinha disponível e, conforme se vês na foto abaixo, constatei que não há diferença aparente entre elas.

A seguir fiz uma série experimentos ao estilo do que vemos no vídeo. Deixei cair cada uma das duas pilhas 60 vezes e registrei a freqüência de “sucessos” (“sucesso” entendo neste caso a pilha acabar parando de pé) em cada série.

Para a pilha “nova” obtive 8 “sucessos” e para a pilha “velha” 11 “sucessos”. Portanto estes resultados configuram que a probabilidade de “sucesso” com ambas as pilhas é baixa (conforme minha expectativa) e que, se nos determos apenas nestas duas AMOSTRAS de 60 lançamentos, parece ser mais provável cair de pé a pilha “velha” do que a “nova”. Cabe aqui a pergunta se esta diferença de 8 para 11 “sucessos” poderia ter ocorrido por acaso. Para responder tal indagação rigorosamente deveríamos proceder um teste de significância estatística para a diferença entre duas frequências. Contentar-me-ei entretanto em calcular a INCERTEZA de cada uma das frequências de “sucesso” – U(f) – que é dada por

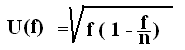
onde f é a frequência observada e n é o número de repetições do experimento.

Para cada uma das duas frequências resulta que as suas incertezas são aproximadamente igual a 3. Conforme aprendemos em textos elementares de Estatística, NÃO se rejeita a hipótese de que a diferença entre as duas frequências observadas tenha ocorrido por acaso se esta diferença (neste caso 3) é inferior cerca de duas vezes a incerteza da diferença entre as duas frequências (aproximadamente 6).

Portanto, além de ser improvável que uma pilha termine de pé na situação do vídeo, NÃO há evidência de que se possa identificar desta forma se uma pilha é “nova” ou é “velha”.

“Docendo discimus.” (Sêneca)

Acessos entre 27 de maio de 2013 e novembro de 2017: 10272.