“Regra da Júlia” para encontrar a raiz quadrada é nova?
21 de novembro, 2023 às 17:17 | Postado em História da Ciência, Matemática, Mitos, empulhações, notícias falsas
Respondido por: Prof. Fernando Lang da Silveira - IF-UFRGSBom dia Professor,
O senhor viu esta reportagem sobre a “regressão de Júlia”? Aluna de 11 anos ajuda a desenvolver fórmula para descobrir raiz quadrada de uma nova maneira
O que sr. pensa sobre a alegação de descoberta da menina Júlia sobre uma nova forma de calcular a raiz quadrada? É realmente uma maneira nova?
Comecemos por explicitar a descoberta da Júlia a partir do exemplo dado na matéria do G1 e em diversos vídeos do YT:
Se tomarmos o quadrado de 10, que é 100, e adicionarmos a soma de 10 com seu sucessor 11, obtemos 121 que é o quadrado de 11.
Se tomarmos o quadrado de 11, que é 121, e adicionarmos a soma de 11 com seu sucessor 12, obtemos 144 que é o quadrado de 12.
Este procedimento foi generalizado por Júlia para qualquer número natural e, portanto, o que a menina descobriu poderia ser denominada “método da Júlia para o cálculo do quadrado de um número natural a partir do quadrado de um número antecessor”.
O “método da Júlia” não vale para se obter a raiz quadrada de um número qualquer mas pode ser usado para encontrar a raiz quadrada de um quadrado perfeito (quadrado de um número natural) partindo-se do conhecimento de outro quadrado perfeito conforme o exemplo indica.
O “método da Júlia” pode ser demonstrado via álgebra (produto notável) e tal foi feito em alguns vídeos do Youtube como segue:
(N +1)2 = N2 + N + (N+1), (1)
onde N é um número natural.
É fácil reconhecer o “método da Júlia” na equação 1 se compararmos com o primeiro exemplo que se encontra no quadro-negro da figura 1:
(10 +1)2 = 102 + 10 + (10+1), (2)
121 = 100 + 10 + 11. (3)
Entretanto o “método da Julia” pode ser demonstrado geometricamente e de fato tal demonstração foi realizada na Antiga Grécia, cerca de 2500 anos atrás. O “método de Júlia” decorre da antiga “regra de Pitágoras” [1] para se encontrar o quadrado de um número natural:
Regra de Pitágoras: o quadrado de um número natural N é igual à soma dos N primeiros números ímpares.
A figura 2 exemplifica a “regra de Pitágoras” para os nove primeiros números naturais.
Se usarmos a “regra de Pitágoras” para calcular o quadrado de onze (primeiro exemplo da figura 1 para o “método da Júlia”) temos:
112 = 1+3+5+7+9+11+13+15+17+19+21, (4)
112 = (1+3+5+7+9+11+13+15+17+19)+(10+11), (5)
112 = (100)+(10+11). (6)
A igualdade 6, consequente da aplicação da “regra de Pitágoras”, resulta no mesmo que a “regra da Júlia”.
A figura 3 apresenta a interpretação geométrica da “regra de Pitágoras” para os primeiros cinco números naturais pois encontrar o quadrado de um número N é calcular a área de um quadrado cujo lado tem extensão N.
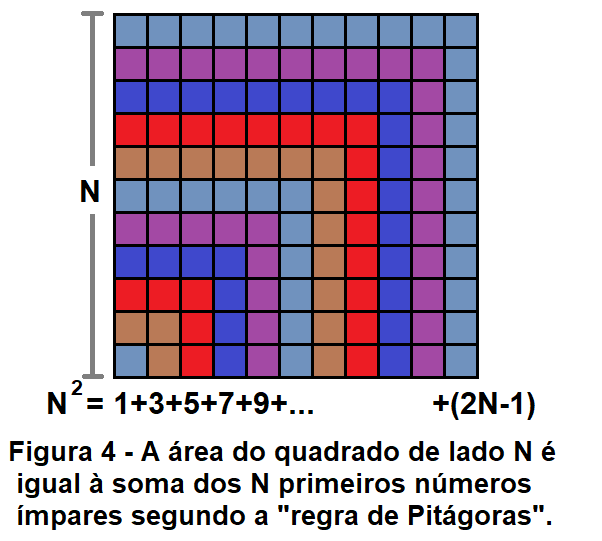
A figura 4 indica o caso geral da “regra de Pitágoras” e sua interpretação geométrica.
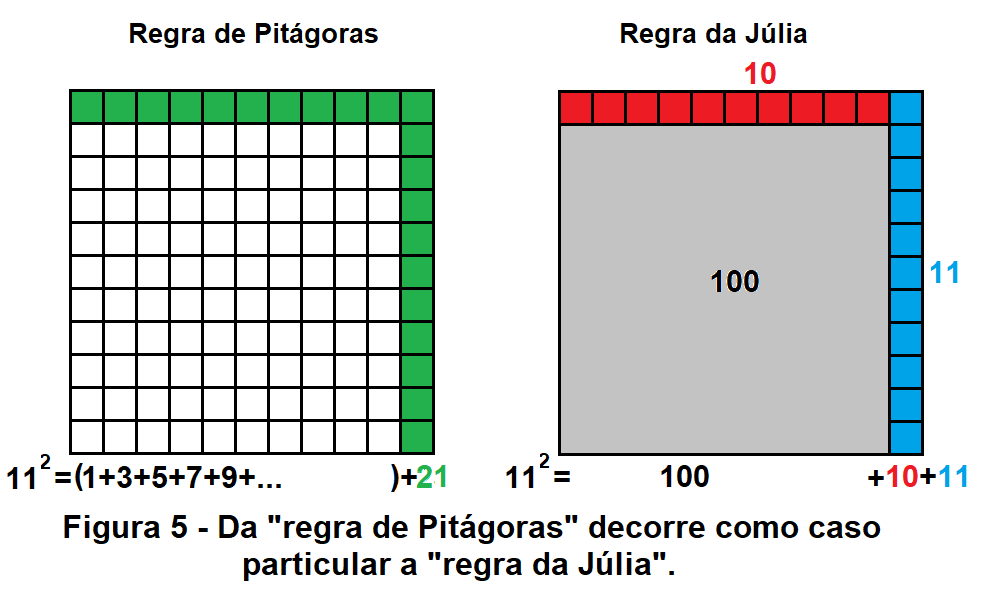
A figura 5 demonstra que a “regra de Pitágoras” implica como caso particular a “regra da Júlia” para o quadrado de 11.
Desta forma, a Júlia redescobriu um conhecimento que remonta aos Antigos Gregos (Pitágoras e outros) cerca de 2500 anos. Isso não desmerece em nada a conquista intelectual da menina.
O surpreendente são as notícias veiculadas pela mídia e repercutida em muitos vídeos do YT de que “tem um jeito novo de calcular raiz quadrada, …”.
Na palestra do vídeo seguinte é discutida a “regra de Pitágoras” e outros temas correlatos: Raciocínios geométricos.
A apresentação utilizada na palestra está disponível no Research Gate.
REFERÊNCIA
Radice, L. L. A Matemática de Pitágoras a Newton. Lisboa, Edições 70, 1971.
“Docendo discimus.” (Sêneca)
Excelente explicação. Fez justiça a Júlia e ponderou sobre vídeos sensacionalistas.
Gostaria de falar que julia eh genial(desculpe o portugues)Muitas pessoas gostariam de desenvolver uma tecnica geral e nao conseguem….Eu sou professor de matematica e nao consigo chegar nisso
Concordas portanto com o que foi dito na postagem.
Acho a aluna,um expoente do Brasil!!
Quando estudei Química, sempre quis saber se existe uma fórmula matemática que preveja o número de elétrons nos níveis da eletrosfera dos átomos, pois tínhamos que decorar a ordem e a quantidade de eléteons em cada nível.
Parabéns à Júlia e ao Prof. Fernando Lang por pelo debate sobre matemática. Eu e talvez milhões de brasileiros aprendemos um pouquinho mais sobre esta ciência tão fascinante e mágica.
Andei apertado meu tempo,agora que aprendi tô fora escola aposentado,mas aprendi a tempo,rsrs
Concordo com a matéria. Desde o início eu achei a veiculação da descoberta sensacionalista. A Júlia teve, sim, um grande mérito, no sentido de que no método adotado, que na realidade consiste em calcular o quadrado de um.número a partir do quadrado do seu antecessor (e não a raiz quadrada), ela utilizou o conceito do quadrado de uma soma (no caso, de n+1), assunto que não é ensinado a alunos de 11 anos. Creio que é assunto da oitava série. Assim, ela mostrou uma habilidade matemática muito além da sua faixa etária. Parabéns à Júlia e mais prudência para quem divulgou o método como uma inovação.
Se já existia esse método e pelo que vi mais fácil de se entender, pq então os professores não começam por ele ao ensinar as crianças? Pq tem que dificultar e fazer os alunos odiarem matemática?
Pq nem eles mesmos sabem !!!
No país que padece entre os piores índices educacionais, esperar tais conhecimentos dos professores, é exigência demais.
Esse sempre foi o meu questionamento, hoje sou estudante do curso de licenciatura em física na UNEB, e penso que facilitar a compreensão dos estudantes fé e uma grande diferença, nem todos nascem gênios, mas não quer dizer que não possam se tornar um.
Muito bom , quero receber essas mennsagens.
Li sobre a redução da Julia a alguns dias e me debruçando na ideia por alguns minutos e percebi que ela decorre diretamente da compreensão geométrica do quadrado e da raiz como o lado do quadrado. Genial? Sim, mas me lembrou do argumento platônico da meniniscencia no Menon. Parecia, simplesmente, que a ideia do cálculo sempre estivera ali, na mente da garota. Faltava apenas o momento de se revelar.
Respondendo a pergunta da Paula, posso dizer, como professor de Matemática que sou, que o fato de não ser ensinado dessa maneira aí tida, como a mais fácil, decorre da mera sequência didática apresentada nos livros didáticos e também tem a ver com a forma como o ensino das raízes de números racionais é ensinada. No mais, a grande maioria dos livros didáticos apresenta 1 ou 2 formas de contextualizar o ensino das raízes com sua representação geométrica.
Então, eu também concordo com a reportagem, mas não tiro o mérito da aluna Júlia, pois esse assunto produtos notáveis não é ensino a alunos com a idade dela. Parabéns, Júlia! Sucesso, menina!
Ufa! A ideia da menina Júlia foi salva e respeitada. Os comentários foram respeitosos e construtivos. Não sou formado, talvez atribua isso ao fato de que em minha idade de escola primária, muitas coisas eram ensinadas de uma forma mais rudimentar e daí advinham enormes dificuldades de compreensão por parte dos alunos. Perto dos oitenta anos, resta_me a alegria e esperança de que nossas crianças e nossos jovens sejam educados e orientados de tal forma que os conhecimentos e os seus domínios sejam tão naturais e essenciais quanto o ar que respiramos. Que todos tenham o direito e as oportunidades para se educarem e serem pessoas felizes e comprometidas com o desenvolvimento de seu país!
Com toda certeza o mérito da aluna não poderia ser menosprezado. Genial. Fico feliz que notícias assim consigam ao menos despertar e renovar a curiosidade em torno do tema. Apesar dos tantos problemas que nossa educação tem, pelo lado da demanda e, como também, da oferta, ainda conseguimos experimentar o que de melhor a educação extrai de nós: o prazer por aprender/ensinar.
Acho a aluna,um expoente do Brasil!!
Olá, mesmo sendo uma redescoberta (e isso o Prof. Lang salientou bem: “não invalida em nada o mérito da aluna”). Eu iria até mais longe: além do mérito da aluna, o seu professor merece os cumprimentos por estimulá-la e por investigar junto. Gostaria de ler seu artigo.
Minha experiência como professor de Matemática: por que não se ensinava dessa forma, já que o método existe há 2500 anos? Existem vários motivos para isso: quase nenhum deles é “incompetência” do professor. Alguém falou na sequência dos livros didáticos: fato! Sem contar que, na grade curricular, as vezes o nível de especificidade é tanto que amarra o professor … Além disso, dentro do universo da Matemática, existem milhões de estudos só no campo da matemática elementar da escola básica. Humanamente não há como saber todos de cor, ainda mais nas condições de trabalho da maioria dos docentes das escolas públicas e também privadas: os professores não têm quase tempo de fazer pesquisa aprofundada.
Sem contar que, assim como essa menina e seu professor provaram, é possível professor e aluno construirem conhecimento juntos (foi o que eles fizeram). Mas isso requer uma mudança de paradigma de ensino-aprendizagem-avaliação, ou seja, das amarras. Caso contrário, teremos apenas casos isolados como esses de vez em quando. E há mais crianças capazes de fazer redescobertas, como a Júlia fez, só precisando um terreno fértil e um professor estimulante.
No que tange a demonstração, é necessário um certo rigor. Eu tomei a liberdade de demonstrar a “regressão de Júlia” por dois métodos: indução e associação com PA. Ambos os métodos validam a construção de Júlia para números de quaisquer tamanhos. Mas isso não foi invenção minha: com certeza vários já fizeram antes de mim. 🙂 Mas a demonstração serve para atestar a validade generalizada. Logo, a regressão de Júlia pode ser usada para calcular a raiz quadrada de um quadrado perfeito com dez milhões de algarismos.