Propagação do som ao longo da coluna de ar atmosférico

7 de abril, 2025 às 20:09 | Postado em Acústica, Atmosfera, Ondas mecânicas

Questão interessantíssima: Qual é a influência da gravidade na propagação de ondas sonoras?

Em 18 anos de sala de aula nunca tinha me deparado com ela.

Professor, e se pensarmos em uma escala maior, a nível atmosférico? Isto é, em uma coluna vertical de ar suficientemente longa teremos a base com maior densidade e o topo com menor densidade. Nesse caso, haveria uma diferença na velocidade de propagação do som? Quão significativa ela seria???

A seção 6 do artigo A Física no salto recorde de Felix Baumgartner abordou a propagação do som na atmosfera e nela me inspiro para dar a resposta.

O valor da velocidade de propagação (rapidez) das ondas sonoras (v_S) depende de duas propriedades do meio onde elas acontecem, da densidade do meio (d) e do módulo de elasticidade volumétrica do meio (K), sendo expressa por

  v_S = (K / d)^1/2 .        (1)

A equação 1  implica em que se apenas a densidade se altera então a onda sonora se propagará com maior rapidez no meio menos denso e não no meio mais denso.

Entretanto no caso particular de um gás, conforme o gás diminui sua densidade (mantido todo o resto constante), diminui o seu módulo de elasticidade volumétrica (ele se torna mais compressível, isto é, para a mesma variação de pressão sofre uma maior variação de volume) e desta forma a razão K divido por d é uma constante. Isto implica que a velocidade de propagação do som em um gás não depende da densidade do gás.

Pode-se demonstrar que a velocidade do som em um gás acaba por depender apenas da temperatura absoluta T, da massa molar M e da razão γ entre os calores específicos molares a pressão e a volume constante do gás de acordo com a expressão que segue:

 v_S = (γ R T / M)^1/2  .    (2)

onde R é a constante universal dos gases.

O ar seco até cerca de 90 km de altitude, conforme se discute em Composição da atmosfera varia com a altitude?, é em quase sua totalidade uma mistura de gases diatômicos (oxigênio e nitrogênio).  Sendo sua massa molar cerca de 28,96 g (0,02896 kg) e sendo a razão entre os calores específicos é 1,4 resulta a equação 2 nas unidades do SI em

 v_S = 20,0 T^1/2 .     (3)

Fica assim demonstrado que ao longo da coluna de ar atmosférico, até cerca de 100 km de altitude, a rapidez da propagação do som depende apenas da temperatura (e não depende da densidade). Entretanto como a temperatura ao longo da coluna de ar varia (vide Temperatura da atmosfera terrestre depende da altitude), a rapidez da propagação do som também mudará.

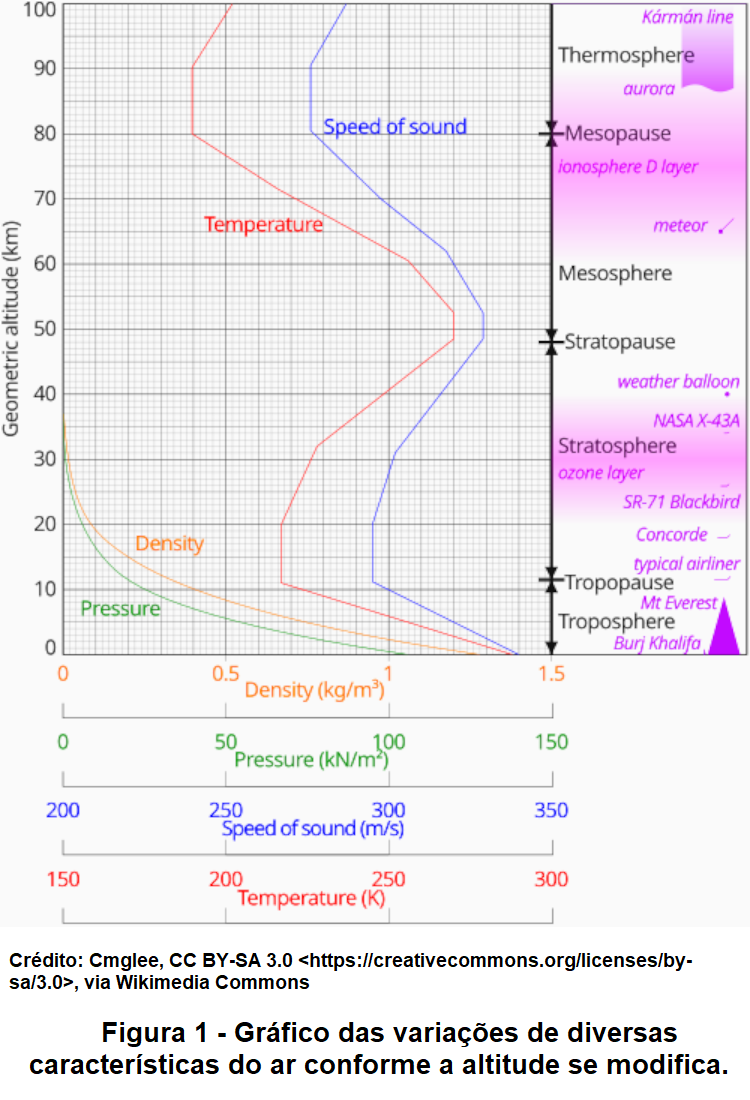
A figura 1 representa diversas características do ar variando com altitude.  Nota-se a variação concomitante da rapidez de propagação do som com a temperatura em acordo com a equação 2.

“Docendo discimus.” (Sêneca)