Processo de aniquilamento entre partícula-antipartícula e conservação de massa
30 de abril, 2021 às 19:26 | Postado em Mecânica, Relatividade
Respondido por: Prof. Nathan Lima (IF-UFRGS)Olá professor, antes de mais nada gostaria de te parabenizar por esse maravilhoso projeto educacional.
Minha dúvida é com relação a um caso específico que podemos observar quando ocorre o contato (colisão, choque, encontro) entre uma partícula e sua antipartícula, como por exemplo o elétron e o pósitron, nesse procedimento observamos o “desaparecimento” de ambos e o surgimento de radiação eletromagnética (fótons), acontecimento esse que pude conhecer através de uma publicação aqui do CREF sobre a equação de Einstein: E=mc2, de modo que também vale salientar que está ocorrendo uma transformação de matéria em onda eletromagnética, e não massa em onda eletromagnética, como também é dito nessa mesma publicação aqui do CREF.
Mas a minha dúvida surgiu na lógica de todo esse fenômeno, ora, seguindo a fala de doutores em física que encontrei pela internet, pude concluir que matéria é tudo aquilo que possui massa, enquanto os fótons, por sua vez, não estão dotados dessa propriedade. E o ponto chave do meu questionamento é o seguinte: Se matéria é tudo aquilo que tem massa, e se transforma em algo que não tem (fóton), somos obrigados a dizer que, mesmo não ocorrendo a ideia sensacionalista e errônea que massa vira energia (sendo que ondas eletromagnéticas por si só nem sequer são energia), ocorreu no fim das contas uma perda de massa… isto é, partículas dotadas de massa simplesmente somem, e surge partículas sem massa, como ficaria a lei de conservação? Este meu questionamento também traz em sua resolução outro conflito que observo muitos entre alguns físicos: A lei de conservação de massa deixa de existir com a relatividade? Se sim, podemos encarar a massa como sendo uma “simples propriedade que o corpo tem ou não, e que quando tem é possível relacioná-la com a energia desse corpo”? Se não, que conclusão podemos tirar do fenômeno de aniquilamento citado acima? Desde já obrigado, ficarei muito grato pela sábia resposta que receber.
A pergunta apresentada é muito interessante e surge a partir de outra resposta presente no CREF (Lima, 2019), como mencionado pelo autor da questão. Complementando, portanto, o texto anterior e buscando responder à presente pergunta, pretendo discutir alguns detalhes sobre o conceito de massa na Teoria da Relatividade Especial.
Primeiramente, vale ressaltar que, na Mecânica Clássica, enuncia-se o chamado Princípio da Relatividade de Galileu, segundo o qual é impossível realizar qualquer teste mecânico que permita saber se um dado referencial está em repouso ou em movimento retilíneo uniforme[1]. No início do século XX, Poincaré (1956)[2] apresentou tal noção como sendo um dos princípios fundamentais da Física. Em 1905, no artigo Sobre a Eletrodinâmica dos Corpos em Movimento, Einstein adota tal Princípio da Relatividade estendendo-o às leis do eletromagnetismo. Juntamente com o princípio da constância da velocidade da luz, conclui-se que o grupo de transformações que relaciona as coordenadas em um sistema de referência S com outro S’, movendo-se com velocidade V em relação ao primeiro ao longo do eixo x, não pode ser o grupo das transformações de Galileu, mas as Transformações de Lorentz:
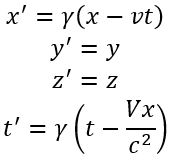
Com
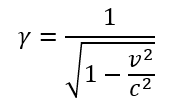
Ao reconhecer as transformações de Lorentz como sendo as transformações corretas, claramente percebemos que o mundo descrito pela Teoria da Relatividade é um mundo muito diferente do mundo descrito pela Mecânica Clássica. Na Mecânica Clássica, espaço e tempo são absolutos, universais e independentes. Na Teoria da Relatividade Restrita, medidas de intervalo espacial e temporal são diferentes em diferentes referenciais inerciais além de dependerem uma da outra. Por descreverem a natureza de forma diferente, Thomas Kuhn (1970) criticava a ideia de que a Mecânica Clássica seria um caso limite da relatividade para baixas velocidades. A Teoria da Relatividade e a Mecânica falam de estruturas diferentes e usam formalismos matemáticos distintos para descrever a natureza, ainda que, em baixa velocidade, você possa obter a mesma previsão teórica para uma determinada medida por ambas as teorias.
Nesse sentido, é natural esperarmos que conceitos da Mecânica Clássica sejam ressignificados na Teoria da Relatividade Especial. Em especial, a forma como a massa é tratada na Teoria da Relatividade Especial é muito diferente do que acontece na Mecânica Clássica. Por exemplo, na mecânica clássica, se você dividir o módulo da força aplicada sobre um corpo pelo módulo da aceleração resultante, você obtém sua massa:

Essa expressão é válida em qualquer referencial inercial e independe do sentido da força. Já na mecânica relativística, se você observa um corpo em movimento e uma força sendo aplicada perpendicularmente a esse movimento, a razão entre o módulo da força e o módulo da aceleração conduz à seguinte expressão:

Se a força, entretanto, for paralela ao movimento, obtém-se a seguinte expressão:

As expressões não são as mesmas! Por conta disso, alguns autores chegaram a propor o conceito de massa transversal e massa longitudinal – um conceito já abandonado na Física. Comento isso, apenas para reforçar que o conceito de massa ganha um sentido muito diferente daquele oferecido na Mecânica Clássica. Com relação à pergunta, especificamente, a energia, na Teoria da Relatividade, continua sendo uma grandeza que sempre se conserva para um sistema fechado em um determinado referencial. A massa, entretanto, pode variar. No caso da aniquilação do par partícula-antipartícula, a energia total do sistema não muda antes e depois da aniquilação; mas a massa muda. Como comentado na resposta anterior (Lima, 2019), a relação entre energia, massa e momento na Teoria da Relatividade Especial é dada por
![]()
Então, aquilo que é “perdido” em massa está presente no momento dos fótons emitidos na aniquilação. Portanto, não há nenhuma violação de uma lei física. Deve-se atentar, entretanto, que o caso de aniquilação é apenas uma situação que torna mais “explícita” a variação da massa. Tal fenômeno somente foi previsto no contexto da Teoria Quântica Relativística, principalmente a partir dos trabalhos de Dirac. Há casos bem mais simples em que a variação da massa já ocorre. Por exemplo, duas partículas que colidem de forma totalmente inelástica (ficando “coladas” após a colisão) têm uma massa maior do que a soma de suas massas iniciais (Duarte e Lima, 2021). Mais especificamente, podemos mostrar que a variação de energia cinética (δK) é responsável pelo aumento de massa (δm) segundo a seguinte equação
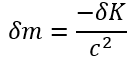
Assim, a energia do sistema se mantém constante; mas aquilo que chamamos de massa se modifica (aquilo que era energia cinética virou energia de repouso). A Prof. Fabiana Kneubil (2018) discute vários exemplos interessantes sobre esse assunto. Isso exemplifica, mais uma vez, como os conceitos de massa e energia, bem como suas relações, são bastante diferentes daquilo que pensamos em termos da Mecânica Clássica.
Agradecimentos
Agradeço à professora Eliane Veit (UFRGS), ao professor Leonardo Heidemann (UFRGS) e ao prof. Sergio Duarte (CEFET-RJ) por uma primeira leitura crítica do texto.
Referências
Duarte S. and Lima N (2021). A simple thought experiment to discuss the mass–energy equivalence in the special theory of relativity . Phys. Educ. 56 035028. Disponível em https://iopscience.iop.org/article/10.1088/1361-6552/abed3b/meta
Kneubil, F. B. (2018). E = mc 2 and the weight of energy. European Journal of Physics, 40(1), 15604. https://doi.org/10.1088/1361-6404/aae7a6
Kuhn, T. S. (1970). Estrutura das revoluções científicas. In Estrutura das revoluções científicas.
Lima, N. W. (2019). Aumento da massa de um corpo quando esse absorve energia. Disponível em https://cref.if.ufrgs.br/?contact-pergunta=aumento-da-massa-de-um-corpo-quando-este-absorve-energia . Acessado em 29 de abril de 2021.
Poincaré, H. (1956). Principles of Mathematical Physics. The Scientific Monthly, 82(4), 165–175. Retrieved from http://www.jstor.org/stable/21942
[1] Essa é uma forma de enunciar tal princípio; mas há outras formas possíveis.
[2] A versão citada é de 1956; mas o texto original é de 1902.

Apenas um comentário que visa complementar a bela explanação do Prof. Nathan: há conversão total de massa em energia mas apenas em processos de aniquilação de pares e portanto em nível quântico. Quando comentamos em aula que 1g de matéria equivale a aprox. 10^14 Joules de energia (10 à potência 14), estamos apenas ilustrando uma idéia, pois não é possível converter toda esta matéria em energia por processos atualmente conhecidos. Em fusão e fissão nuclear apenas uma fração da massa é convertida em energia (como na fusão de hidrogênios no Sol – a fusão nuclear – ou a fissão de urânio nos reatores nucleares). Na aniquilação de pares, esta conversão é de 100%. Quando se afirma “ondas eletromagnéticas por si só nem sequer são energia” devemos ter cuidado com a afirmação pois sim, elas não são energia mas transportam não apenas energia mas também momento. Isso explica por um lado o fato de recebermos energia do Sol via ondas eletromagnéticas e do conhecido fenômeno da pressão de radiação. Um outro fato importante mas que vai um pouco além da pergunta feita: na Teoria da Relatividade Geral é amplamete sabido que a energia de ondas eletromagnéticas (ou por exemplo a energia de ligação de átomos) têm propriedades gravitacionais, ou seja, elas entram nas Equações de Campo de Einstein da mesma maneira que a massa inercial m entra. Por isso a distinção massa vs. energia em Relatividade Geral perde um pouco do seu sentido clássico.
(Prof. Silvio Dahmen)
Agradeço pela postagem e oelo comentario de Silvio Dahmen. Queria ressaltar que não conhecia estea deralhes da critica de Kuhn, oor exemplo. MS goataria de fazer uma pergunta adicional: ainda que a fração de enerfia liberada por colisões inelasticas na forma de calor e som seja deaprezível, elas levam um pouci da energia não? Aquela fórmula – delta m =delta K/c² seria um casol ideal, não?
Agradeço antecipadamente