Princípio da Incerteza

11 de julho, 2024 às 13:08 | Postado em Mecânica quântica

Os livros texto apresentam o Princípio da Incerteza como decorrência da perturbação que o ato de medida introduz quando se observa algo como o elétron. Tal abordagem está correta?

O princípio da incerteza, é um princípio fundamental da moderna física quântica, tendo sido apresentado pela primeira vez por Werner Heisenberg em um artigo  1927 [1],   considerando o que ocorreria ao utilizar um microscópio hipotético utilizando raio gama para observar um elétron. Sendo o raio gama uma radiação com menor comprimento de onda do que a da luz, este hipotético microscópio permitiria determinar com uma precisão δx muito menor a posição do elétron do que seria possível com um microscópio ótico. Utilizando o conceito de fóton, a radiação gama ao interagir com o elétron, causa um desvio no mesmo (este efeito já havia sido estudado mas com raio x por  Arthur Compton) resultando em uma imprecisão no momento linear δp devido a imprecisão inicial na posição  do elétron. No artigo Heisenberg demostra que estas imprecisões, utilizando a mecânica quântica resultam na desigualdade [2]

δxδp≥ℏ/2.

E destaca que [1]

Assim, quanto maior a precisão na determinação da posição, menor será a precisão na determinação do momento.

Ou dito de forma mais usual, a medida da posição tem como consequência uma perturbação imprevisível e não controlável na medida do momento linear. Da forma apresentada por Heisenberg, temos uma relação entre perturbações devido à realização de medidas no sistema.

Esta é a maneira que o Princípio da Incerteza é apresentado em alguns livros-texto muito utilizados no Brasil, principalmente nas disciplinas iniciais. Por exemplo, a figura 1 é do livro de Física Quântica, de R. Eisberg e R. Resnick, que ilustra exatamente  a abordagem de Heisenberg.

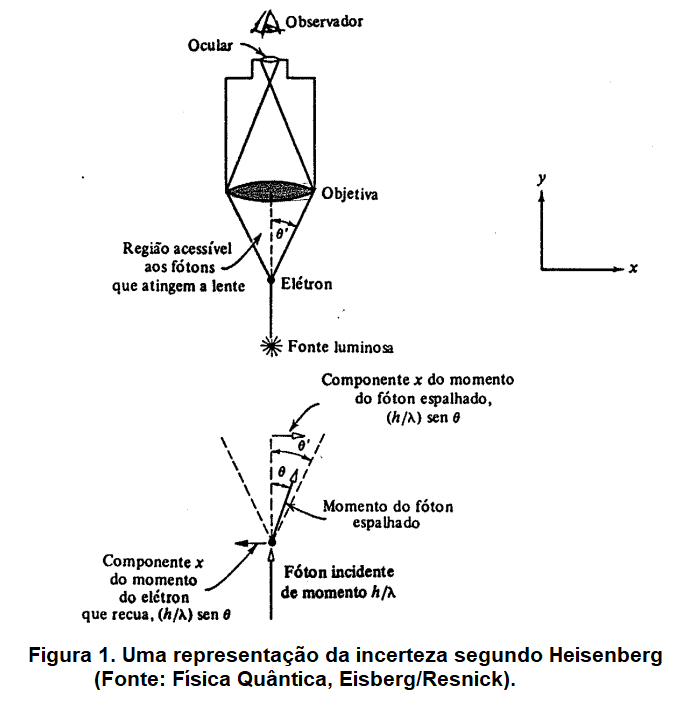
No entanto, a equação do Princípio da Incerteza é apresentada nos livros, utilizando uma versão desenvolvida por E.H. Kenard em 1927, generalizando o resultado de Heisenberg,

ΔxΔp≥ℏ/2

Mas qual a diferença entre as duas? Seriam apenas de notação?  Existe uma diferença importante a primeira (a de Heisenberg) expressa a precisão das medidas (uma limitação nas medidas) e a segunda expressa o desvio padrão (decorrente das limitações na preparação do estado utilizado nas medidas) [3].  É possível obter a primeira equação a partir da segunda, mas a inversa não é possível.  A equação obtida por Kenard é rigorosamente alicerçada no formalismo da mecânica quântica, a de Heisenberg não é deduzida a partir do formalismo da mecânica quântica. A figura 2, retirado de [3], ilustra a diferença ente o desvio padrão (neste texto Δq é representado por Δx) e incerteza na medida. O que denominamos Princípio da Incerteza , é a segunda equação , e não  a primeira.

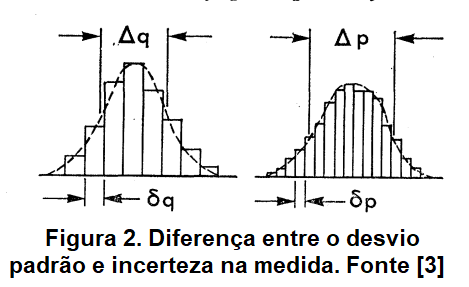
Uma questão que pode surgir é como podemos ter uma incerteza menor que o desvio padrão, não teríamos problemas com a violação do Princípio da Incerteza? Ou a interpretação de “incerteza de medida” como desenvolvido por Heisenberg não seria correta?

Em relação a esta questão,  M. Ozawa [4] apresentou uma dedução da relação original

δxδp≥ℏ/2

de Heisenberg, mas com um procedimento mais rigoroso, obtendo [5]

δxδp+Δxδp+Δpδx≥ℏ/2

Uma consequência interessante desta relação é que passa a ser possível realizar medidas precisas na posição, que viola a desigualdade proposta por Heisenberg. E dois artigos publicados em 2012 [6], utilizando técnicas diferentes, mostraram a violação da Princípio da Incerteza proposto por Heisenberg, mas satisfazendo a generalização proposta por Ozawa.  Estes resultados demonstram que é possível reduzir as incertezas nas medidas SEM violar o Princípio da Incerteza.

Para evitar confusões, o que os experimentos demonstram é a violação da relação [7],

δxδp≥ℏ/2

 e não da relação

ΔxΔp≥ℏ/2

de forma que o Princípio da Incerteza, que relaciona os desvios padrões continuam válidas. O que os experimentos e o artigo de Ozawa mostram é que a proposta de que o Princípio da Incerteza limita as precisões das medidas como costuma ser apresentado em alguns livros-texto, não é correta. Algo que precisa ser corrigido!

Notas e referências

[1] O artigo de Heisenberg traduzido para o inglês, está reproduzido no livro Quantum Theory and Measurement, John Archibald Wheeler (Editor), Wojciech Hubert Zurek (Editor), Princeton University Press,

[2] A equação no artigo de Heisenberg é deduzida considerando um pacote de onda gaussiana, mas aqui estamos considerando um estado genérico. No caso de pacote gaussiano, a incerteza é mínima.

[3] Veja por exemplo o artigo de Ballentine, Statistical Intepretations of Quantum Mechanics ou a referência [4].

[4] Ver M. Ozawa,  Universally valid reformulation of the Heisenberg uncertainty principle on noise and disturbance  in measurement

[5] No artigo de Ozawa, a dedução é realizada para um par arbitrário de operadores.

[6] Os artigos publicado no PRL Violation of Heisenberg’s Measurement-Disturbance Relationship by Weak Measurements ou com acesso livre aqui e o artigo publicado na Nature  Experimental demonstration of a universally valid error–disturbance uncertainty relation in spin measurements com acesso livre aqui .

[7] Lembrando que as medidas não envolveram posição e momento, mas a ideia é semelhante para os pares de grandezas utilizadas em cada caso. Se você conhece sobre operadores e comutadores, a fórmula geral do Princípio da Incerteza para é dado por

ΔA^ΔB^≥12|⟨[A^,B^]⟩|

para dois operadores arbitrários. Note que para operadores que comutam, o limite inferior é zero.