Período do pêndulo em um sistema de referência acelerado

9 de junho, 2017 às 9:13 | Postado em Forças inerciais, Mecânica

Professor, se um pendulo sobe um plano inclinado com aceleração constante, qual seria o seu período?

Eu darei uma resposta mais abrangente imaginando um pêndulo em um sistema de referência acelerado (portanto em um sistema de referência não-inercial) e sujeito também a um campo gravitacional e depois particularizarei para o caso do sistema acelerado no plano inclinado. Aliás, todas as nossas experiências cotidianas são em um sistema de referência acelerado devido ao fato de que a Terra descreve uma rotação diariamente e portanto qualquer sistema de referência solidário à Terra está acelerado. Quando experimentamos com pêndulos, exceto nos polos da Terra, estamos em situação não-inercial.

Cabe um comentário relevante sobre o significado de “g” na bem conhecida equação que fornece o período do pêndulo, isto é,

T = 2π (L/g)^1/2 .

A letra “g” nesta equação designa a aceleração de queda livre (aceleração da gravidade) no sistema de referência onde o pêndulo se encontra. E como é bem sabido, a aceleração de queda livre NÃO é idêntica à intensidade do campo gravitacional a não ser que o sistema de referência considerado fosse inercial (não acelerado). Vide a postagem Por que PESO não deve ser tomado como sinônimo de FORÇA GRAVITACIONAL?

No caso específico de considerarmos o sistema de referência na Terra, a orientação e a intensidade de “g” é obtida somando-se a intensidade do campo gravitacional com a aceleração centrífuga, aceleração que decorre do efeito inercial no sistema de referência da Terra – em módulo ela é idêntica à aceleração do sistema de referência que gira em torno do eixo de rotação da Terra, a bem conhecida aceleração centrípeta,  mas aponta para fora do eixo de rotação da Terra (tem sentido contrário à aceleração do sistema de referência não inercial). Vide a postagem
Força centrífuga e Rotação da Terra e centrifugação .

Vou particularizar esta discussão do período do pêndulo para o caso do equador terrestre. Como ali a intensidade do campo gravitacional é aproximadamente 9,81m/s² e a aceleração centrífuga no equador é 0,03 m/s²  é fácil concluir que a g=9,78m/s² . Em outros pontos da superfície da Terra é um pouco mais difícil a obtenção do valor de “g” pois a orientação da intensidade do campo gravitacional (que aponta para o centro da Terra se a modelamos como um distribuição esférica de massa) é diferente da orientação da aceleração centrífuga já que esta aponta para fora do eixo de rotação da Terra e diminui de intensidade conforme muda a latitude.

No caso do teu questionamento teremos que calcular uma nova aceleração da gravidade no sistema de referência que se desloca aceleradamente plano inclinado acima,  somando o vetor aceleração da gravidade na superfície da Terra (que já incorpora o efeito inercial devido à rotação da Terra) com um vetor aceleração que tem o mesmo módulo da aceleração plano inclinado acima mas com o sentido invertido. Este novo valor de “g” será então usado para calcular o período de pêndulo acelerado plano inclinado acima.

A figura abaixo representa à esquerda a aceleração da gravidade no sistema de referência da Terra (g_T) e a aceleração do pêndulo plano inclinado acima. À direita indica a composição das duas acelerações na obtenção da nova acleração da gravidade no sistema de referência acelerado plano inclinado acima. Nota que neste caso resulta um vetor g com intensidade maior do que a do vetor g_T  e desta forma o pêndulo oscilará com menor período. Outro aspecto a ser destacado é que a direção de g não coincide com a de  g_T, determinando que o pêndulo oscilará em  torno dessa nova direção.

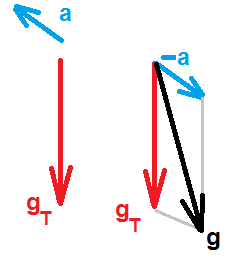
É instrutivo imaginar o que aconteceria com um pêndulo na Estação Espacial Internacional. Como a sua aceleração (a) é idêntica em módulo direção e sentido a g_T, o novo valor de g é nulo. Ou seja, o pêndulo está em microgravidade e não oscilará. Vide Microgravidade é o mesmo que gravidade nula?

Finalmente destaco que desde o início do meu raciocínio estou usando o Princípio da Correspondência que afirma que um sistema de referência acelerado (não-inercial) é equivalente a um sistema de referência inercial em presença de um campo gravitacional.

“Docendo discimus.” (Sêneca)

Visualizações  entre 27 de maio de 2013 e novembro de 2017: 596.