Lei de Benford – Um exemplo com dados sobre a população brasileira
19 de agosto, 2021 às 20:09 | Postado em Estatística e probabilidade, incertezas experimentais, Matemática
Respondido por: Prof. Lucas W. da S. Crispim e Prof. Luiz C. M. de Aquino - Depto. de Ciências Exatas - FACSAE/UFVJM - Campus MucuriCaros professores
Gostaria que os senhores fizessem um artigo sobre a Lei Benford com algum exemplo de sua aplicação em um conjunto de dados da realidade.
Agradeço antecipadamente
A Lei de Benford foi observada primeiramente pelo astrônomo e matemático Simon Newcomb. No final do século XIX, Newcomb notou que as páginas de um livro contendo tabelas de logaritmos com valores referentes aos números começando com o algarismo 1 eram mais gastas do que as páginas com valores referentes aos números começando com o algarismo 2 (e assim por diante para os demais algarismos). Esse fato levou Newcomb a pensar que a ocorrência do algarismo 1 como primeiro dígito num conjunto de dados aleatório era mais frequente do que os demais. Em meados de 1940 o engenheiro eletricista e físico Frank Benford retomou os trabalhos de Newcomb. Benford testou as ideias de Newcomb contra 20 conjuntos de dados e publicou um artigo acadêmico verificando uma lei. Apesar do trabalho de base feito por Newcomb, o Benford acumulou grande parte do crédito pela descoberta da lei e agora ela é comumente referida como “Lei de Benford”. Em meados de 1990 o matemático Theodore P. Hill [1] publicou o trabalho intitulado “A statistical derivation of the significant-digit law” no qual provou matematicamente o fenômeno por trás dessa lei.
A Lei de Benford afirma que em determinados conjuntos numéricos a frequência do algarismo 1 aparecendo como primeiro dígito dos elementos será maior do que a frequência do algarismo 2, que por sua vez será maior do que a frequência do algarismo 3 e assim por diante até chegar no algarismo 9. Essa lei sugere que a probabilidade de um algarismo d aparecer como primeiro dígito será igual a log(d + 1) – log(d). Por exemplo, a probabilidade de aparecer o algarismo 1 é aproximadamente 30,1%, de aparecer o algarismo 2 é 17,6%, de aparecer o algarismo 3 é 12,5%, etc. Vide a Tabela 1 para encontrar as probabilidades de cada algarismo.
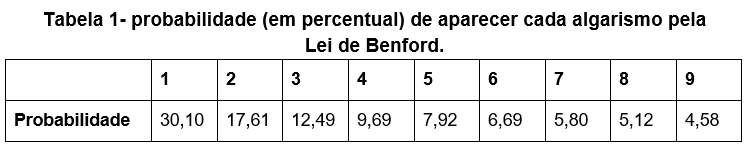
Um exemplo da aplicação da Lei de Benford é na quantidade da população por município em um determinado país. Neste texto faremos um experimento utilizando os dados do Instituto Brasileiro de Geografia e Estatística (IBGE) [2] para verificar essa lei na população dos municípios brasileiros considerando a estimativa de 2020. Nós calcularemos a frequência absoluta do primeiro dígito do valor da população de cada município e em seguida vamos determinar “quão próximo” essa frequência está dos valores previstos pela Lei de Benford. Para realizar essa comparação vamos analisar o erro percentual entre o valor da frequência e o valor esperado pela lei. No processamento dos dados utilizamos a linguagem de programação Python e o código está disponível no repositório [3].
O erro percentual Ei será calculado conforme a equação (1), onde o índice i é o algarismo, ei é a frequência absoluta esperada e oi é a frequência absoluta observada na amostra dos dados.
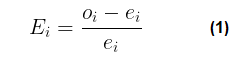
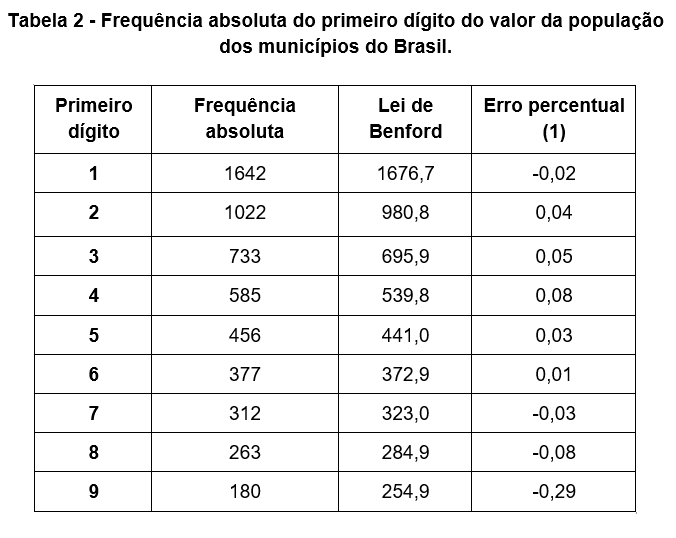
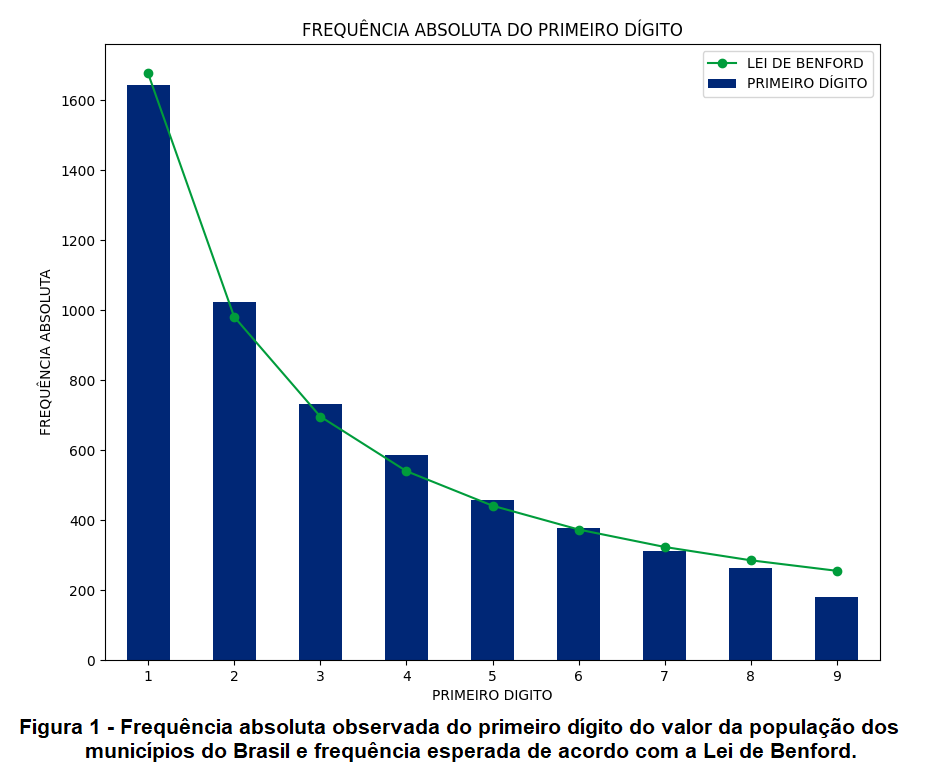
Na Tabela 2 temos a frequência absoluta do primeiro dígito do valor da população dos 5.750 municípios do Brasil em 2020. Notem que o maior erro em módulo ocorreu para o algarismo 9. Entretanto, exceto para esse algarismo, o erro ficou em 8% para mais ou para menos. Podemos dizer que o valor previsto pela Lei de Benford tem uma aproximação razoável com a frequência absoluta calculada. Na Figura 1 temos uma comparação visual entre a curva da lei e o gráfico de barras da frequência.
Vale mencionar que naturalmente nem todos os conjuntos de dados vão seguir a Lei de Benford. Por exemplo, vamos considerar a altura (em centímetros) dos adultos em um determinado país. Como um ser humano adulto tem altura que pode variar entre pouco menos de 100cm até pouco mais de 200 cm, analisando a frequência dos algarismos no primeiro dígito da altura, vamos encontrar predominantemente os algarismos 1 e 2. Isso claramente vai desobedecer a lei de Benford. Nesse sentido, para que essa lei possa ser aplicada o conjunto de dados em questão precisa ter duas características básicas:
1) qualquer um dos algarismos 1, 2, 3, …, 9 pode aparecer no primeiro dígito de cada amostra;
2) as amostras nesse conjunto devem ter uma alta ordem de grandeza entre seu valor mínimo e seu máximo.
Notem que no caso dos municípios do Brasil teremos essas duas características básicas. Em relação à característica 2), a ordem de grandeza será de 107, pois com a menor população temos Serra da Saudade (MG) com 776 habitantes, enquanto que com maior população temos São Paulo (SP) com 12.325.232.
Referências
[1] Hill, Theodore P. “A Statistical Derivation of the Significant-Digit Law”. Statistical Science 10, no. 4 (1995): 354-63. Disponível em: <http://www.jstor.org/stable/2246134>. Acesso em: 18 ago. 2021.
[2] Estimativas da População. 2020. Disponível em: <https://www.ibge.gov.br/estatisticas/sociais/populacao/9103-estimativas-de-populacao.html>. Acesso em: 18 ago. 2021.
[3] Aquino, Luiz C. M. de, Crispim, Lucas W. da S. Lei de Benford e a população do Brasil. 2021. Disponível em: <https://github.com/lcmaquino/lei-de-benford-populacao-br>. Acesso em: 18 ago. 2021.

Esta lei tb nao ajuda nao deteccao de fraudes?
Sim. Alguns exemplos encontram-se em Aplicações.
Sim. Temos um artigo com esta aplicação :
https://doi.org/10.1016/j.physa.2017.12.120
Vale salientar, caro amigo Fernando Lang, que a lei de Newcomb-Benford se aplica apenas a dados que NÃO são adimensionais. Portanto, os valores numéricos dos dados aplicáveis dependem das unidades. Se existe uma distribuição de probabilidade universal P (x) sobre tais números, então ela deve ser invariante sob uma mudança de escala, então, embora esta não seja uma distribuição de probabilidade adequada (uma vez que diverge). Assim, tanto as leis da Física quanto as convenções humanas impõem limites que ainda precisam ser conhecidos.
Resumindo, falta-nos ainda um claro modelo físico que esclareça o motivo de seu funcionamento na Natureza. Para situar o problema do ponto de vista epistemológico, ele é algo semelhante a se usar as conhecidas leis ponderais da Química, empiricamente descobertas, ANTES de se dispor da Teoria Atômica que lhes confere um significado mais inteligível e palatável.
Para os matemáticos, isso até pode parecer irrelevante, mas não para os físicos que relacionam a ordem matemática com a natureza.
Há um episódio do Fronteiras da Ciência sobre este assunto:
http://frontdaciencia.blogspot.com/2017/10/lei-de-benford.html