Gravitação: sistema binário

13 de setembro, 2015 às 10:48 | Postado em Astronomia, Gravitação, Mecânica

Professor Lang em uma situação de planeta binário, não se pode aplicar a terceira lei de Kepler em relação ao centro de massa? Para relacionar os períodos, se não porque?

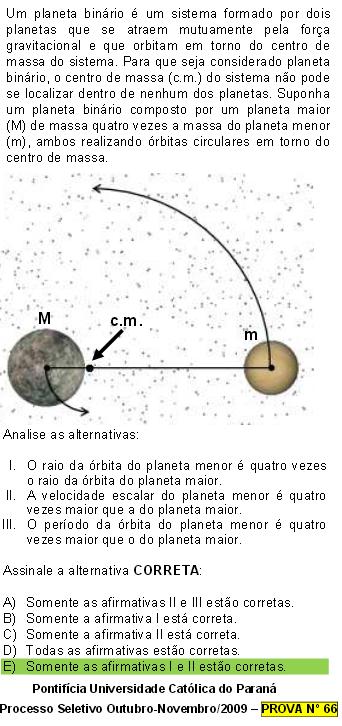
Eu encontrei isso em uma questão, ele definia sistema binário da seguinte forma:  “Um planeta binário é um sistema formado por dois planetas que se atraem mutuamente pela força gravitacional e que orbitam em torno do centro de massa do sistema. Para que seja considerado planeta binário, o centro de massa (c.m.) do sistema não pode se localizar dentro de nenhum dos planetas”. O que me chamou atenção foi que segundo o gabarito que foi dado a banca considerava que esses dois planetas giravam como se fossem um halter, com mesma velocidade angular. Porém, quando fiz algumas contas para relacionar a situação com a Lei dos Períodos do Kepler já não se encontrava essa situação. Queria saber se de fato uma situação dessa não se pode aplicar a 3ª Lei de Kepler usando como ponto de referencia o centro de massa dos dois planetas. Obrigado

Questão na íntegra abaixo:

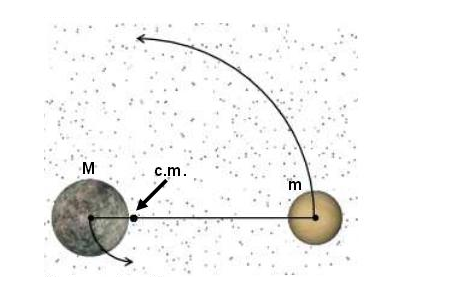
Este é um problema de DOIS CORPOS interagindo gravitacionalmente. As forças gravitacionais são forças internas ao sistema e, portanto, não podem alterar o momento linear total do sistema. No sistema de referência do centro de massa dos dois planetas as velocidades (lineares) dos dois planetas devem ter a cada momento a mesma direção, sentidos contrários e os seus valores (os módulos das velocidades) devem estar na razão inversa das massas dos planetas para que o centro de massa esteja em repouso. Ou seja, como o planeta menos massivo tem massa quatro vezes menor do que a massa do planeta maior, sua velocidade deve ter módulo quatro vezes maior do que o módulo da velocidade do outro planeta.

Para um sistema como este, as órbitas de cada planeta em torno do centro de massa podem ser elípticas ou circulares. O enunciado afirma que elas são circulares. Ora, se elas são circulares e o centro de massa está sempre em repouso, o centro das órbitas é o centro de massa dos dois planetas, ou seja, eles devem descrever trajetórias circulares com iguais velocidades angulares em torno do centro de massa.

De fato aplicaste a Lei dos Períodos de Kepler fora do domínio de validade. A lei, como a conheces, poderia ser aplicada se os dois planetas estivessem orbitando graças às forças gravitacionais exercidas por um terceiro corpo com massa muito maior do que a massa dos planetas. De acordo com este problema as órbitas são decorrentes da força gravitacional mútua ENTRE os dois planetas e isto leva a que a Lei dos Períodos de Kepler não possa ser usada como aconteceu em teu raciocínio.

Finalmente é importante destacar que as Leis de Newton são mais gerais do que as Leis de Kepler. No primeiro parágrafo de minha resposta eu utilizei as Leis de Newton.

Outras postagens sobre gravitação: Gravitação

“Docendo discimus.” (Sêneca)

Visualizações entre 27 de maio de 2013 e novembro de 2017: 1160.