Exemplificação do Teorema Central do Limite na soma de 5 variáveis aleatórias

27 de agosto, 2015 às 9:24 | Postado em Estatística e probabilidade, incertezas experimentais, Matemática

Esta postagem decorre de um material que preparei para a disciplina de “Métodos Quantitativos aplicados à Pesquisa em Ensino de Física”, oferecida aos mestrandos e doutorandos do Programa de Pós-Graduação em Ensino de Física do Instituto de Física da UFRGS.

Dedico esta postagem especialmente aos alunos da turma do segundo semestre de 2015.

O objetivo da postagem é uma exemplificação do Teorema Central do Limite através da simulação de variáveis aleatórias pelo Método de Monte Carlo.

O Teorema Central do Limite afirma que a soma (S) de N variáveis aleatórias independentes (X), com distribuição e variâncias semelhantes,  é uma variável com distribuição que se aproxima da distribuição de Gauss (distribuição normal) quando N aumenta.

Adicionalmente a média de S é o somatório das médias de X e a variância de S é a soma das variâncias de X.

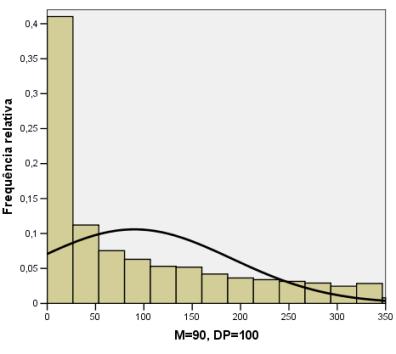
A seguir são apresentados histogramas para cinco variáveis aleatórias com distribuições NÃO gaussianas (que não obedecem a distribuição de Gauss ou normal) simuladas pelo Método de Monte Carlo. A cada um dos histogramas está ajustada uma curva normal com o objetivo de caracterizar a violação de normalidade para as distribuições das cinco variáveis geradas. A média (M) e o desvio padrão (DP) de cada uma das variáveis também são informados.

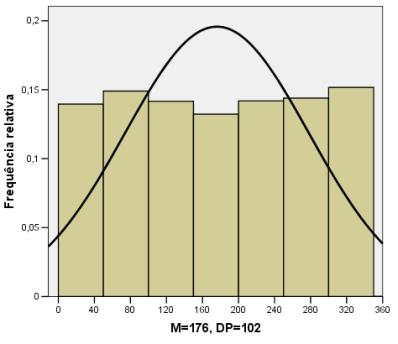
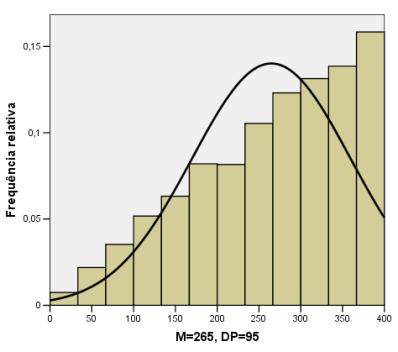
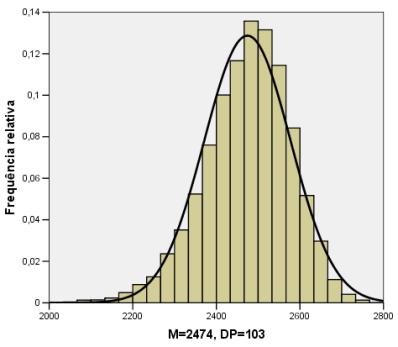
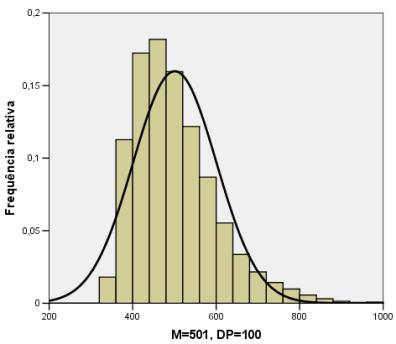
A seguir é apresentado o histograma para a variável obtida da soma das cinco variáveis anteriores. A curva normal ajustada a esta última distribuição indica que esta distribuição é com excelente aproximação gaussiana, exemplificando assim o importante  Teorema Central do Limite.

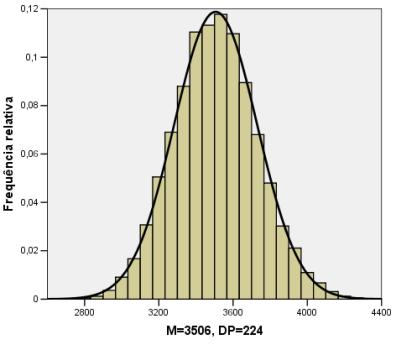
Verifica-se também que a variável SOMA das cinco variáveis apresenta MÉDIA igual a soma das MÉDIAS das cinco variáveis:

M = 176 + 265 + 2474 + 501 + 90 = 3506

Igualmente verifica-se que a variável SOMA das cinco variáveis apresenta VARIÂNCIA igual a soma das VARIÂNCIAS das cinco variáveis:

VAR = 102² + 95² + 103² + 100² + 100² = 50038

DP = 50038^1/2 = 224

Vide também Exemplificações do Teorema Central do Limite na distribuição das médias amostrais

Uma apresentação contendo todas as simulações das duas postagens se encontra disponível no ResearchGate. Ao final da apresentação também disponibilizo as sintaxes para reproduzir duas das simulações com o pacote SPSS.

Vide outras postagens sobre o Teorema Central do Limite.

“Docendo discimus.” (Sêneca)

COMENTÁRIOS EM 22/05/2018

Visualizações entre 27 de maio de 2013 e novembro de 2017: 957.