Direção da velocidade angular pode ser diferente da direção do momento angular?

5 de março, 2018 às 18:52 | Postado em Dinâmica da rotação, Mecânica

Professor,  poderia me dar um exemplo de um caso em que momentum angular e velocidade angular não tem mesma direção e sentido? Ou será que o meu professor de Física 1 se equivocou ao afirmar isso? E se estiver correto, então é necessário um torque resultante para manter um corpo girando com velocidade angular constante?

É fácil demonstrar que em um sistema tão simples como um haltere constituído por duas partículas ligadas por uma haste leve, girando em torno de um eixo leve e  inclinado em relação à haste (vide a figuras1 e 2), o momento angular não coincide com a velocidade angular. Pela definição de momento angular – produto vetorial do vetor posição da partícula pelo seu momento linear – sabe-se que ele é sempre perpendicular ao plano determinado pelo momento linear de uma partícula e o vetor posição da partícula em acordo com a regra da mão direita. Nas figura 1 e 2 os momentos lineares das partículas (em vermelho) são perpendiculares ao plano determinado pela haste e pelo eixo de rotação e os vetores posição tem origem no centro de massa e se estendem até os locais das partículas.

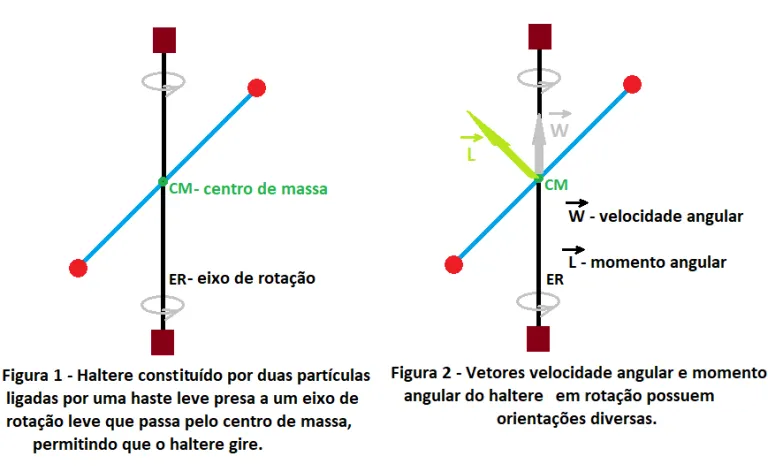
Somente em circunstâncias especiais os dois vetores velocidade e momento angular são coincidentes. É fácil para um haltere que gira descobrir qual deve ser a orientação da barra em relação ao eixo de rotação para que tal ocorra.

Como o momento angular do haltere muda de orientação enquanto gira então deve haver um torque externo ao sistema pois o somatório de todos os torques sobre um sistema é a taxa de variação (derivada temporal) do momento angular do sistema. A figura3 representa par de forças externas (binário) exercidas pelos pivôs sobre o eixo de rotação do sistema.

COMENTÁRIOS ADICIONAIS:

A inércia de rotação é descrita por um TENSOR 3 por 3. Ou seja, os conhecidos momentos de inércia (discutidos em livros de Física 1) são apenas três das nove componentes do TENSOR DE INÉRCIA de um corpo rígido. As demais componentes são os chamados produtos de inércia (usualmente varridos para baixo do tapete em Física 1). A resultante dos torques sobre um corpo rígido em rotação é o produto do tensor de inércia e da velocidade angular.

A diagonal principal do tensor é constituída pelos momentos de inércia segundo os eixos x, y e z. Os demais elementos da matriz são os produtos de inércia.

Em Física Geral 1 já me dou por MUITO satisfeito   quando os alunos entendem o que é momento de inércia e aprendem a tratar de situações muito especiais envolvendo rotações. O restante talvez (?) algum dia aprendam em uma disciplina de Mecânica Racional (esta denominação só os mais velhos conhecem), Mecânica Clássica, Mecânica Analítica, … . Minha estreia em 1973 como professor universitário na UNISINOS (graduei-me em 1972) foi em Mecânica Racional II. 

Outras postagens sobre movimento de rotação em Rotação do corpo rígido.

“Docendo discimus.” (Sêneca)