Condensando resultados experimentais de uma mesma grandeza com diferentes incertezas

18 de maio, 2021 às 16:11 | Postado em Estatística e probabilidade, incertezas experimentais, Matemática

Prof. Lang,

em um experimento de fenda dupla o espaçamento entre as fendas (d) foi determinado medindo-se a posição dos dois primeiros máximos e mínimos, levando aos seguintes resultados, em metros: (2966±2)x10^-8; (2970±1)x10^-8; (2962±4)x10^-8  e  (2902±1)x10^-8.

Qual a melhor estimativa que se pode fazer para o valor de d, com a respectiva incerteza, a partir das quatro medidas?

Muitíssimo obrigada pelo esclarecimentos, que passarei diretamente aos meus alunos. (Quem sabe eles também se tornem fãs do Pergunte ao CREF.)

Eliane

Quando existem diversos medidas ou resultados experimentais relativos a uma mesma grandeza, cada um deles expresso por um valor central e sua respectiva  incerteza, é importante antes de mais nada verificar se esses resultados são coerentes entre si ou se ocorrem medidas discrepantes. Uma forma de analisar a consistência dos resultados é  construir um gráfico de barra de erro com eles. A Figura 1 é o gráfico para os quatro resultados da medida do espaçamento d da fenda dupla, onde cada barra está centrada no valor estimado para d e se estende por uma incerteza acima e abaixo deste valor.

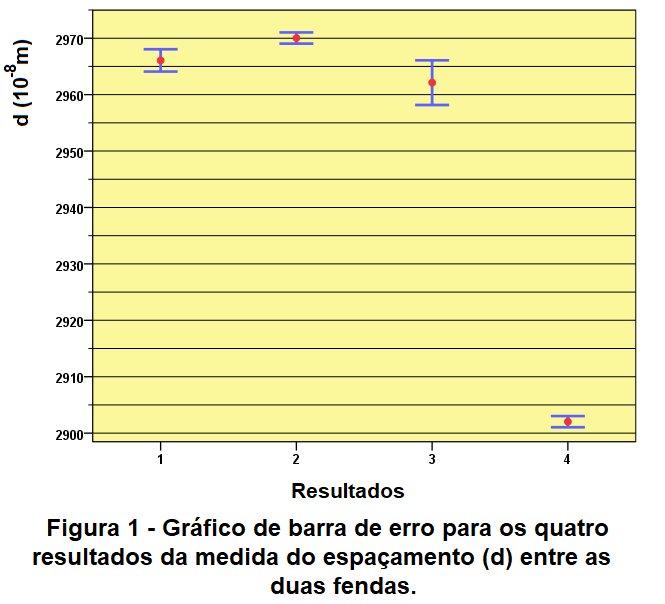
A simples inspeção visual do gráfico permite identificar que os três primeiros resultados são consistentes entre si pois as diferenças entre os três valores centrais de d se assemelham às suas incertezas. Entretanto o quarto resultado se afasta dos demais por distâncias muito maiores do que as incertezas, caracterizando que ele é um outlier e merece ser colocado a parte dos demais[1]. Nesta análise ele será simplesmente descartado mas em outras circunstâncias o experimento  e os cálculos que o produziram poderiam  ser refeitos para tentar identificar alguma falha ou até algum erro de grosseiro.

Os procedimentos a seguir visam condensar os três primeiros resultados em um único, levando ao valor final para d com sua respectiva incerteza.

A condensação dos diversos valores experimentais é usualmente feito por uma média aritmética. A média aritmética simples é adequada quando todos os resultados experimentais são homocedásticos ou igualmente confiáveis mas ela não é a melhor a opção no caso de incertezas experimentais diferentes entre si, no caso de  heterocedasticidade das medidas. 

É intuitivo que resultados com menor incerteza devam ser privilegiados em relação aos demais. Ou seja, uma média aritmética ponderada é então preferível a uma média aritmética simples. A média aritmética ponderada para os três resultados experimentais de interesse está dada na equação 1 (é fácil generalizar esta equação para um número qualquer de termos) onde o peso de cada resultado é indicado pela letra ρ:

A equação 1 se reduz à média aritmética simples caso os três pesos sejam iguais a 1/3.

A incerteza propagada (u) para a função advinda da média ponderada é dada pela equação 2:

Um critério para se chegar ao peso de cada um dos resultados é os ponderando pelo inverso de quadrado de sua incerteza. Desta forma, quanto maior é a incerteza de um particular termo, menor será sua contribuição para o resultado final. As equações 3 a 5 expressam os pesos de cada um dos três resultados:

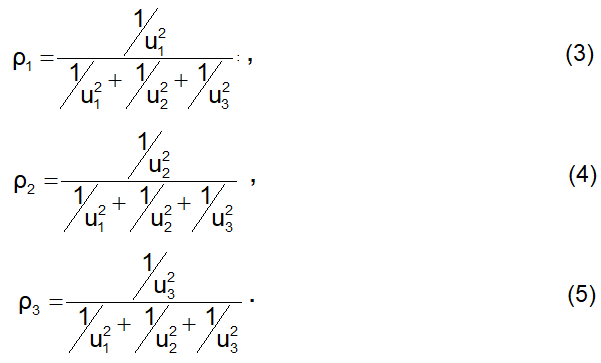
A substituição dos valores das incertezas nas equações 3 a 5 fornecem  os pesos no caso em pauta:

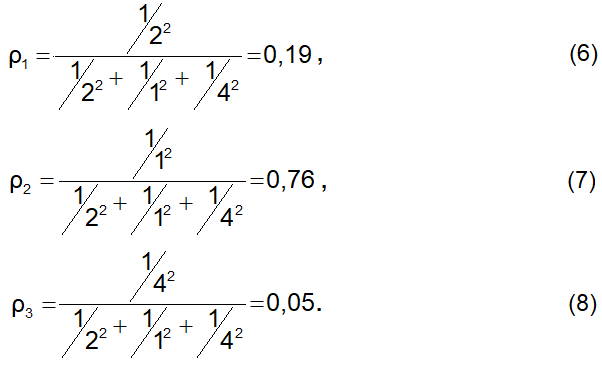
Substituindo-se na equação 1 os três valores da distância entre as duas fendas e os respectivos pesos encontra-se o valor final para d que tem como unidade de medida 10^-8m:

Substituindo-se os pesos e as incertezas na equação 2 encontra-se a incerteza do resultado final que tem como unidade de medida 10^-8m:

Desta forma o resultado final é:

Se a média aritmética simples dos três resultados fosse utilizada ao invés da média aritmética ponderada se encontraria como resultado final

que é semelhante ao encontrado em (11). Entretanto o resultado dado em (12)  apresenta incerteza maior do que aquela obtida com a média ponderada pois os pesos privilegiaram as medidas com menores incertezas.

[1] – Em uma abordagem mais rigorosa os quatros resultados seriam submetidos a uma Análise da Variância (ANOVA) visando inicialmente identificar se há diferenças estatisticamente significativas entre eles e, se existirem, localizar as diferenças e as medidas discrepantes.

“Docendo discimus.” (Sêneca)