Como Eratóstenes mediu 7° entre Assuã e Alexandria para achar a circunferência da Terra?
24 de janeiro, 2015 às 7:34 | Postado em Astronomia, Filosofia da Ciência, Forma da Terra, História da Ciência, Mítica Terra Plana
Respondido por: Prof. Fernando Lang da Silveira - www.if.ufrgs.br/~lang/Professor, como Eratóstenes conseguiu medir 7° entre Assuã e Alexandria para descobrir a circunferência da Terra?
Eratóstenes (276 a.C. – 194 a.C.) usou o fato de que no solstício de verão o fundo de um poço em Siene (hoje Assuã) era iluminado pela luz solar ao meio dia. Tal acontece, no solstício de verão, pois Siene se situa no hemisfério norte, praticamente sobre o Trópico de Câncer. Poços profundos e estreitos somente podem ter o seu fundo iluminado pela luz solar se estiverem em latitudes que ficam entre os dois paralelos dos trópicos. Aqui em Porto Alegre NUNCA um poço vertical profundo terá seu fundo iluminado pois aqui, como em qualquer latitude maior do que a dos trópicos, o Sol NUNCA se encontra no zênite. Vide O movimento anual e diário do Sol quando referido à Terra.
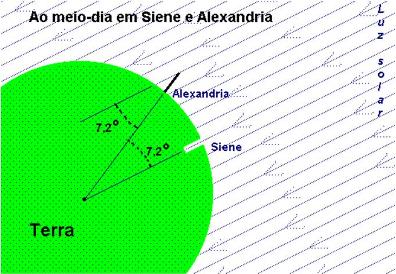
A cidade de Alexandria está praticamente ao norte de Siene e portanto em Alexandria no solstício de verão o Sol NÃO está no zênite. Um estaca cravada verticalmente em Alexandria, ao meio-dia no solstício, projeta uma sombra cerca de 8 vezes menor do que a altura da estaca. Ou seja, a luz do Sol ao meio dia tem uma orientação que perfaz um ângulo de aproximadamente 50 vezes menor que o ângulo subtendido pela circunferência, isto é, cerca de 7,2°.
Desta forma, Erastóstenes usando o tamanho da sombra, ao meio dia, de uma estaca cravada verticalmente em Alexandria quando no mesmo momento em Siene o Sol estava no zênite, concluiu que a distância entre as duas cidades é 50 vezes menor do que a circunferência da Terra.
Os bematistas, povo que se dedicava à agrimensura, fizeram a medida da distância entre Siene e Alexandria, encontrado cerca de 5.000 estádios. Portanto, a conclusão de Eratóstenes é de que a circunferência da Terra é cerca de 50 vezes 5.000 estádios, isto é, aproximadamente 250.000 estádios.
Os historiadores não sabem com precisão qual era a extensão de um estádio, avaliando-a em cerca de 0,16 km. Assim, nas unidades atuais a circunferência da Terra para Erastóstenes vale aproximadamente 0,16 x 250.000 km = 40.000 km. Ora, este resultado é muito próximo do que de fato sabemos hoje sobre tal medida.
Cabe ainda alguns comentários sobre esta medida de Erastóstenes.
– Os valores atribuídos a Eratóstenes, reportados por Cleomedes, eram aproximados, além de que, o raciocínio de multiplicar por 50 a distância entre as duas cidades somente é válido se elas estiverem sobre o mesmo meridiano. Apesar de não ser rigorosamente verdade é uma excelente aproximação para Alexandria (longitude de 30° Leste) e Siene (longitude de 32° Leste).
– Um pressuposto relevante é de que a Terra seja esférica. Ou seja, experimento não prova que a Terra é esférica (Eratóstenes tinha diversas evidências da esfericidade) e o objetivo do mesmo era calcular a circunferência da Terra e não provar que a Terra é esférica.
– Outro pressuposto importante, além de a luz solar se propagar em linha reta, é de que o Sol está muito distante da Terra. Isto é, que a distância Terra-Sol seja muito maior do que o raio da Terra. Na época de Eratóstenes tal suposição estava sujeita a críticas, embora Aristarco de Samos (310 a.C – 230 a.C.) já ter determinado a distância Terra-Sol em cerca de 1500 raios terrestres (vide Determinação da distância Terra-Sol na antiga Grécia).
Finalmente, os mesmo dados que Eratóstenes empregou para determinar a circunferência da Terra, outro filósofo, Anaxágoras (conforme medidas de espaço-PEF ) utilizou em um modelo de Terra plana, para avaliar a distância Terra-Sol. Vide figura abaixo.
Cerca de um século após a determinação de Eratóstenes, Posidônio (135 a.C – 51 a. C.) realizou uma medida independente da circunferência da Terra. A estrela Canopus, visível em Rodes (cidade onde ele vivia) apenas próxima do horizonte, era visível ao sul em Alexandria com elevação máxima de cerca de 7,5 graus. A partir da distância entre Rodes a Alexandria (conhecida de maneira pouco fidedigna) e da suposição (errada) de que ambas as cidades se encontram sobre o mesmo meridiano, obteve algo em torno de 35 mil km para a circunferência da Terra. Vide o artigo “Sobre a forma da Terra”.
Relacionado com a hipótese anacrônica no século XIX em diante de a Terra ser plana existem diversas tentativas inconsistentes para a determinação da distância Terra-Sol no mundo mundo mítico dos terraplanistas. Vide
Distância ao Sol na mítica Terra Plana: a razão de as diversas estimativas serem conflitantes!
Mais um exercício terraplanista de dissociação cognitiva na determinação da distância Terra-Sol
Medida do raio terrestre por Eratóstenes
Vídeos que tratam do tema: Carlos Machado, MarceloAndarilho.
“Docendo discimus.” (Sêneca)
Visualizações entre 27 de maio de 2013 e novembro de 2017: 3786.

Muito esclarecedor! Eu uso as evidencias de Eratóstenes e Aristarco de Samo e Aristóteles para refutar a hipótese da terra plana. Apesar de que atualmente por motivos que não sei existe poucos estudiosos da área ( como o Dr. Afonso formado em geofísica) que querem provar uma terra plana. Mas isso me faz estudar mais em busca da verdade ou solidifica- la . Gostaria de ter mais acesso com senhores sobre essas questões. Sabemos que a ciência se preocupa em trabalhar sobre métodos racionais para determinar a validade dos resultados e que esta sujeita a mudança desde que esta seja a verdade sobre a realidade e não a minha ou a sua verdade do mundo pluralista.
Refutações da mítica Terra Plana não faltam e podes encontras diversas em Mítica Terra Plana
Especialmente sobre um entre tantos exercícios de dissociação cognitiva do professor exonerado da USP vide Tamanho da Terra em foto da NASA: prova de que a foto é falsa?
O trabalho original do Eratóstenes perdeu-se na noite dos tempos,não sabemos exatamente como ele fez a medida da Terra.A fonte segundária é o livro “Meteora” do Cleomedes.Segundo Cleomedes,Eratóstenes usou um tipo de relógio solar chamado SCAPHE ,uma bacia com um gnomom no centro,para medir os ângulos das sombras.De todo modo,o mérito do Eratóstenes ,segundo alguns autores,foi o de fazer os experimentos, em vez de ficar só nas conjecturas.
OBS: Eratóstenes não utilizava medidas babilônicas para ângulos.
Cálculos matemáticos JAMAIS PROVARÃO A FARSA DO GLOBO GIRATÓRIO.
A Terra sempre foi plana. A Gravidade é uma grande FARSA, pois ninguém até hoje conseguiu provar a gravidade com EXPERIMENTOS REAIS. Só na ficção existem pessoas vivendo de cabeça para baixo numa bola giratória.
Para começar a Terra NUNCA foi plana. A concepção de Terra plana está superada no século V a.C. mas ressurge entre fideístas ignorantes no século XIX.
Em segundo lugar ninguém vive de cabeça para baixo em qualquer ponto do planeta a não ser plantando bananeira e por pouco tempo. Mas que um antípoda tem a sua vertical rotacionada de 180 graus um em relação a outro é fácil verificar e até terraplanistas já fizeram belas demonstrações disso mais de uma vez, comprovando que a Terra é esférica. Uma delas está discutida em Duas terraplanistas demonstram em um vídeo que a Terra NÃO é plana!.
LUA VISTA DO JAPÂO E DO RIO DE JANEIRO
Mais sobre a MITOLOGIA TP em MÍTICA TERRA PLANA
O trabalho original de Eratóstenes perdeu-se na noite dos tempos.Segundo Cleomedes,livro “Meteora”,Eratóstenes usou um tipo de relógio solar chamado “SCAPHE”,uma bacia com gnomom no centro para achar a medida da Terra.O grande mérito de Eratóstenes,segundo alguns autores,foi o de fazer experimentos e não ficar só nas conjecturas.
Obrigado,gosto muito dessa página.
Como Eratóstenes sabia que, ao mesmo tempo, havia sombra em Alexandria, mas não havia sombra em Siene (700km depois) ???? Como ele descobriu isso? Como foi comunicado?
Em um manuscrito da grande biblioteca de Alexandria, onde Eratóstenes era o bibliotecário, ele encontrou a informação de que o Sol se encontrava praticamente no zênite, iluminando o fundo poço de Assuã (então Siena) no solstício de verão.
Como Eratóstenes mediu simultaneamente as duas varetas, uma em Siena outra em Alexandria, distantes 800 km sem utilizar um rádio transmissor, sendo que ao meio dia o relógio solar marca nas duas cidades inexistência de sombra. Sombra em Alexandria resulta não ser meio dia.
Agora, pra ser exata a experiência e ao mesmo tempo (mesmo instante) nas duas cidades uma com sombra e outra sem sombra ele precisava ter um rádio transmissor. Nenhum relógio daquela época poderia garantir o mesmo instante. Era meados de 100 a.C, não era?
Ele não mediu simultaneamente pois fez apenas uma medida. No dia em que o Sol ao meio-dia iluminava o fundo poço em Sienne (este dia era conhecido e estava registrado em documentos da Biblioteca de Alexandria!), mediu o comprimento da sombra ao meio-dia em Alexandria.
Como em 100 ou 200 anos antes de Cristo alguém poderia medir ao meio dia uma vareta (relógio solar) com sombra? Se ele mediu em Alexandria ao meio dia e tinha sombra, não poderia ser meio dia. Meio dia não tem sombra.
Estás redondamente equivocado como é o usual entre os terra-chatos. ?
Se o Sol está a pino, no zênite, ao meio-dia em um particular local da Terra, ele não está no zênite ao meio-dia em outras localidades com diferentes latitudes.
Aqui em Porto Alegre, assim como em qualquer latitude maior do que a dos trópicos, o Sol NUNCA está no zênite ao meio-dia. Portanto o teu comentário é um disparate de quem não conhece o básico sobre o mundo onde vive.
Também me faço estas perguntas.
Estes experimentos já foram reproduzidos no nosso tempo?
Milhares de alunos do primeiro grau realizam todos os anos, em diversos locais do globo, o experimento no Projeto Eratóstenes. Em pelo século XXI é salutar ter dúvidas mas mais salutar ainda é utilizar a internet para, por contra própria, as resolver. 😉
Sandro, eis a explicação:
O exato instante (meio-dia) é aquele em que a haste produz a menor sombra em ambas as localidades.
Antes do meio-dia a sombra vai diminuindo, e, após, aumentando. De modo que é possível marcar o tamanho da menor sombra em ambas as localidades, sendo aquele o exato instante do meio-dia.
Em outras palavras, a cidade egípcia mais ao sul, Siena, atualmente Assuã, situa-se praticamente no mesmo paralelo do Trópico de Câncer, e, no dia e hora do solstício de verão no hemisfério norte, o Sol, ao meio-dia, ”a pino” (zênite), iluminava praticamente todo o fundo do poço em Siena (ou seja, zero sombra numa haste posicionada na vertical, a prumo). Enquanto que em Alexandria, ao norte e ligeiramente a oeste , naquele mesmo instante verificava-se uma sombra na haste que seria a sombra de menor projeção ao longo do dia. Essa sombra de menor projeção em Alexandria indicava que na altura do Trópico de Câncer próximo àquele meridiano (em Siena) o Sol estava “a pino”. Um pouco antes ou um pouco depois, a sombra da haste fincada em Alexandria seria maior.
Portanto, zero sombra em Siena e a menor projeção de sombra da haste em Alexandria ocorriam necessariamente no mesmo instante (ao meio-dia, naquela faixa de meridianos).
Finalmente vejo alguém mencionar que ele não provou a esfericidade, que no caso é um pressuposto. Até Carl Sagan e Marcelo Gleiser dizem que ele provou. Abs.
Infelizmente lhes faltava maiores informações da história da ciência. A esfericidade da Terra está posta antes de Eratóstenes.
Acho fabuloso o resultado obtido por eratóstenes mas me pergunto como ele garantiu a sincronia das medidas (que é fundamental para assegurar a confiabilidade do resultado)?
Não há sincronicidade das medidas pois há apenas uma medida feita por Eratóstenes. Era sabido que no solstício de verão, ao meio-dia, o Sol estava a pino em Siena (Assuã) pois lá era iluminado o fundo de um poço. Em um solstício de verão, ao meio-dia, Eratóstenes mediu a sombra de uma estaca em Alexandria.
É triste saber que há pessoas que tentam desmerecer estudos e experiências realizadas pelas antigas civilizações. Essas pessoas se esquecem de que ninguém nasce sabendo e que todos bebem dos conhecimentos dos antepassados, nem quer for pelo menos meia dose . É de Eratóstenes, o famoso Crivo que leva o seu nome, com o qual é possível exprimir números primos, agora, imagine se ele tivesse uma calculadora eletrônica ou um computador XT naquela época.
Oi pessoal, esse cálculo do diâmetro da terra faço com meus alunos sempre nos solstícios e equinócios. Uma maneira de comemorar estas datas. A estratégia é conectar alunos de escolas distantes 50Okm, aqui na Bahia é fácil, pelo tamanho do estado.
Usamos cabos de vassouras 1,4m, e trena. No mesmo horário, 15h, medimos simultaneamente a projeção da sobra nos dois lugares. Pronto!
Ah, tomamos as distâncias pelo Google map. O cuidado é que o diâmetro encontrado é de um circulo passando pelo dois pontos do esferoide. Se a orientação for L-O a 15 S é muito menor que o diâmetro máximo como na linha do equador.
Ah! não tenho paciência para explicar que a terra não é plana para humanos acima de 9 anos. Tô sem paciência!
Para terra-chatos de fato, isto é, para reacionários fundamentalistas religiosos de algumas seitas pseudo-cristãs, os argumentos não funcionam pois estão blindados pelo Domo da Ignorância Fideísta. Para incautos e desinformados, não blindados, vale o esforço de esclarecimento.
Eu não gostei.
Porque não explica nada com que eu quero saber.??
Se esta postagem não explica o que gostarias de saber, continua tua busca. Existem muitos materiais sobre Eratóstenes disponíveis na internet.
A Terra é plana .
Estás redondamente enganado! 🙂
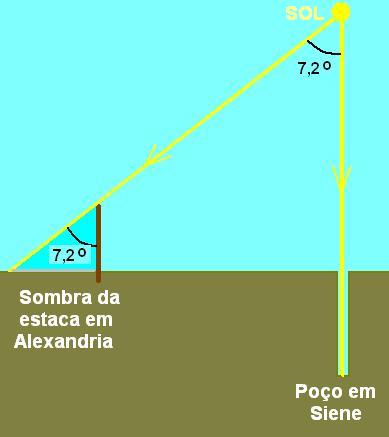
Eu estou procurando como ele chegou a essa medida de 7,2°. Não vi isso no texto. Qual foi a conta que o fez concluir que era 7,2°?
Eratóstenes mediu o comprimento da sombra de um gnomon ao meio-dia. Sabendo a altura do gnomon e o comprimento da sombra, calculou o ângulo.

Abaixo um gnomon triangular.