Calendário se repete a cada 28 anos?

11 de janeiro, 2024 às 12:32 | Postado em Matemática, Mitos, empulhações, notícias falsas

Está correta a afirmação de que nosso calendário se repete a cada 28 anos?

Vamos primeiro definir o que significa “calendário se repete”. Significa que se dois  anos começam no mesmo dia da semana e o último dia do ano também ocorrem na mesma semana para ambos os dois anos, o calendário é repetido.

Podemos verificar isto de forma relativamente simples. Vamos considerar um ano com  365 dias, isto implica que temos 52 semanas mais um dia em um ano. Isto que dizer que se o dia primeiro de janeiro é um domingo, o dia 31 de dezembro será também um domingo.  Assim, o outro ano inicia em uma segunda-feira e o ano termina em uma segunda-feira, e assim sucessivamente até que no sétimo ano o calendário iniciaria novamente em um domingo, e o calendário voltaria a repetir e a sequência se manteria sendo retomada a cada sete anos. Na tabela 1 apresentamos um exemplo, começando com um ano arbitrário, que definimos como ano 1. Anotamos o dia da semana que o ano inicia e o dia da semana que o ano termina.

Mas estamos esquecendo de um detalhe importante, os anos bissexto! A cada 4 anos  precisamos acrescentar um dia ao ano. E isto implica que no quinto ano, o deslocamento será  de dois dias e não de um dia da semana. Quando consideramos os anos bissextos, para que ocorra uma repetição do calendário, a o período não é mais a cada sete anos.  Considerando um ano de 365,25 dias, temos um total de 52 semanas  mais 1,25 dias. Para ocorrer a repetição é necessário multiplicar 1,25 por um número inteiro de tal forma que o resultado seja um múltiplo inteiro de 7 ,os dias das semana, ou seja precisamos resolver a equação 1,25p=7q, de forma que p/q seja um número inteiro. Fazendo  a conta, encontramos que p/q=5,6. Como p,q são números inteiros,  encontramos que a cada 28 anos  o calendário se  repete.

Será verdade? Se olharmos por exemplo o ano de 2017, que começa em um domingo e termina em um domingo, encontramos que em 2023, o mesmo acontece. E o intervalo de tempo não é de 28 anos! O que está errado?

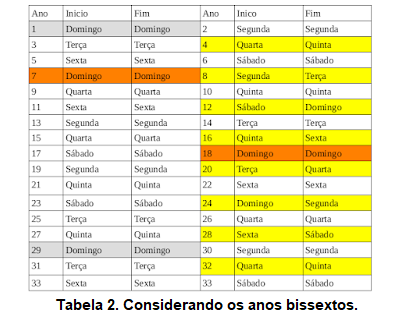
Nada está errado. De fato, o calendário pode se repetir em períodos menores que 28 anos, mas a sequência completa, ela se repete a cada 28 anos. Na tabela 2 repetimos o procedimento utilizado para construir a tabela 1, agora incluindo os anos bissextos, que estão destacados com um fundo amarelo. Note que o correspondente ao ano 1 (domingo-domingo) ocorre novamente no ano 7 e no ano 18 (marcados com fundo laranja), mas note que o ano 2 é diferente do ano 8 e ano 19. Mas iniciando no ano 29, tudo se repete, notando que o ano 30 é igual ao ano 2,o ano 31 é igual ao ano 3 e assim sucessivamente.

O que denominamos período é o intervalo de tempo para toda sequência voltar a ocorrer, isto não quer dizer que uma pequena parte da sequência não possa aparecer dentro do período. Por exemplo, considere a seguinte sequência de números

1,2,3,5,6,7,1,3,4,5,6,1,2,3,4,6,7,1,2,4,5,6,7,2,3,4,5,7

1,2,3,5,6,7,1,3,4,5,6,1,2,3,4,6,7,1,2,4,5,6,7,2,3,4,5,7

1,2,3,5,6,7,1,3,4,5,6,1,2,3,4,6,7,1,2,4,5,6,7,2,3,4,5,7

    Notemos que a sequência completa repete a cada 28 números (que destacamos em cores diferentes), mas por exemplo o número 5 aparece com intervalo menor que a cada 28 números [1].  Então o que ocorre com nosso calendário é algo parecido, a periodicidade de uma sequência ocorre a cada 28 anos, mas isto não implica que para que o calendário seja repetido sejam necessários aguardar 28 anos.

 Mas o período de 28 anos, também não é correto! Por que? Quando calculamos os anos bissextos, a cada 100 anos, o ano não será bissexto, exceto se for múltiplos de 400 anos. Fica como uma diversão, tentar determinar como ocorrem as repetições dos calendários considerando estas condições de 100 e 400 anos.

   Nota

[1] A sequência representa exatamente o que ocorre com o calendário. Cada número representa o dia da semana que o ano inicia (por exemplo 1 é domingo, 2 é segunda-feira e assim sucessivamente). Você pode utilizar uma sequência semelhante para responder o desafio do que ocorre se consideramos os períodos de 100 e 400 anos. Se você sabe por exemplo utilizar uma planilha, consegue facilmente programar a construção da sequência numérica.