Aceleração gravitacional relativa entre dois corpos
12 de fevereiro, 2015 às 8:56 | Postado em Gravitação, Mecânica
Respondido por: Prof. Fernando Lang da Silveira - www.if.ufrgs.br/~lang/Sempre se diz que todos os corpos “caem” com a mesma aceleração/velocidade; Na superfície da Terra, cerca de 9,8 m/s². Isto é parcialmente verdade. Todos os corpos são, de fato, acelerados à mesma velocidade em direção à Terra, mas a própria Terra é acelerada a acelerações diferentes em relação a corpos de massas diferentes. Assim, corpos mais massivos levam menos tempos para alcançar a superfície da Terra. É claro que, para os pequenos corpos com que lidamos, esta diferença é desprezível. Pense em objetos tão massivos quanto à Lua, Vênus ou o Sol. Será que o Sol e a Terra, se estivessem em queda livre, um em direção ao outro, se aproximariam com a aceleração gravitacional da Terra? Porque não prevaleceria a do Sol? Na verdade, O Sol é acelerado em direção à Terra com aceleração gravitacional da Terra, e a Terra, em direção ao Sol com a aceleração gravitacional do Sol; Assim, os corpos caem com a soma das acelerações! Estou correto?
Incialmente um reparo na própria pergunta. Pareces confundir velocidade com aceleração. A afirmação correta é que corpos com diferentes massas próximos à superfície do planeta caem com a mesma ACELERAÇÃO, o que significa dizer que suas velocidades VARIAM e, portanto, qualquer afirmação sobre velocidades depende das condições iniciais da queda e do tempo.
Vou contextualizar minha resposta para o sistema Terra-Lua. A aceleração induzida na Lua pela força gravitacional entre a Terra e o seu satélite é aproximadamente 3 mm/s^2 enquanto que o planeta é acelerado pela Lua por cerca de 0,03 mm/s^2. Estas acelerações explicam que ambos os corpos descrevam um movimento aproximadamente circular (na verdade elíptico) em torno do centro de massa do sistema Terra-Lua, situado abaixo da superfície do planeta.
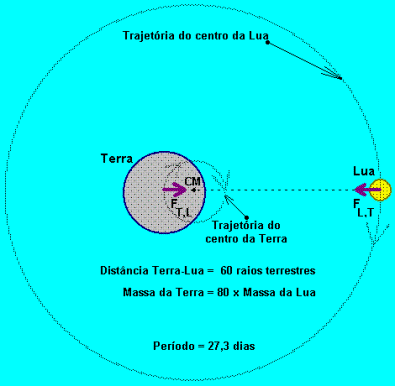
Portanto a aceleração relativa Terra-Lua, que rigorosamente tem um valor que é a soma dos dois valores (3 e 0,03 mm^2), acaba por resultar em cerca de 3 mm/s^2. Nota portanto que mesmo para tal sistema a aceleração relativa é semelhante, se diferencia muito pouco da aceleração que a Lua tem em relação ao centro de massa do sistema.
Um fato interessante é que o Sol acelera ambos os corpos a cerca de 6 mm/s^2, portanto cerca do dobro da aceleração que a Lua sofre por parte da Terra. A propósito de a ter a força gravitacional do Sol na Lua o dobro do valor da força que a Terra lhe aplica cabe a pergunta Por que a Lua não escapa?, respondida no endereço http://www.if.ufrgs.br/cref/?area=questions&id=76.
A aceleração gravitacional resultante da Terra, por exemplo, será portanto a soma (vetorial) de todas as acelerações gravitacionais sofridas pela Terra.
Sobre uma importante perturbação causada pelo campo gravitacional do Sol sobre o sistema Terra-Lua vide Rotação da linha apside Terra-Lua: por que acontece?
“Docendo discimus.” (Sêneca)
Acessos entre 27 de maio de 2013 e novembro de 2017: 1977.

Pensando-se no sistema Terra-Lua, a Lua não deveria cair na Terra, uma vez que seu movimento em direção ao centro da Terra é acelerado pela gravidade? Ademais, por que a aceleração centrípeta seria como qualquer outra aceleração? Não me parece que uma mudança no módulo de uma velocidade seja equivalente a uma mudança na direção de uma velocidade. Ambas, portanto, parecem ser muito distintas.
Qualquer corpo em órbita circular em torno da Terra está sempre “caindo”, isto é, se afastando da reta tangente ao seu movimento em um dado momento, se aproximando portanto do centro de força.
O caso da órbita da Lua é mais complicado pois ela é elíptica e, portanto, há momentos em que a Lua efetivamente se aproxima da Terra e em outros momentos ela se afasta. há muitas postagens tratando do nosso satélite no CREF e sugiro acessá-las em LUA.
Quanto ao comentário sobre a variação em direção da velocidade vide Variação da velocidade no MCU.