A orientação do vetor de Poynting e a direção de propagação da onda

10 de agosto, 2022 às 17:54 | Postado em Eletromagnetismo, Ondas eletromagnéticas, Óptica, Radiação

O vetor de Poynting necessariamente aponta na direção de propagação da onda?

Não necessariamente. O vetor de Poynting, que define o fluxo de energia de um campo eletromagnético, é frequentemente representado como paralelo à direção de propagação de uma onda eletromagnética (OEM). Porém, há situações especiais em que isso não ocorre e começamos vendo um exemplo. Na Figura 1 temos a propagação de um feixe de uma frente de onda plana (1a) comparado ao que possui momento angular orbital (1b).

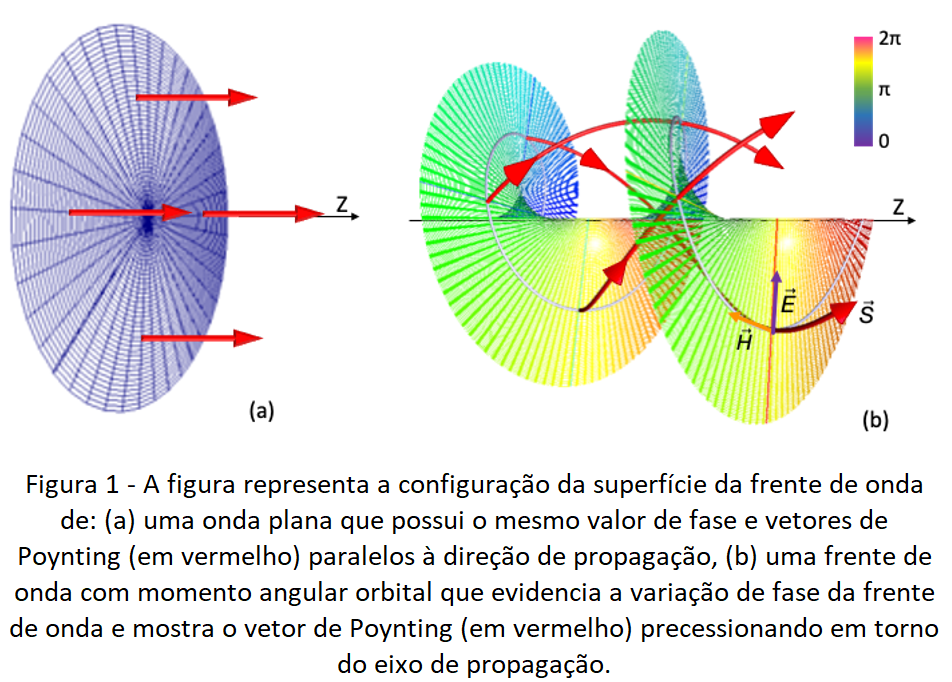
Um feixe como o da fig 1b propaga na direção Z, mas possui uma frente de onda de superfície helicoidal com uma singularidade contida em um eixo, i.e., ali o valor dos campos da OEM é nulo. Observa-se ainda que nestas ondas os campos e estão contidos na superfície helicoidal e que, assim, o vetor de Poynting resultado do produto , agora precessiona em torno do eixo, i.e., em torno do eixo de propagação da onda. Veja que o fluxo líquido de energia correspondente à propagação da onda, continua a ser paralelo à direção de propagação, ou ainda, correspondente à componente de  ao longo de Z (), e que a componente azimutal de  representa sempre um fluxo total nulo através de qualquer superfície fechada.

A definição baseada no produto vetorial entre os campos elétrico e magnético – – está diretamente relacionada à figura de conservação de energia através de uma relação de continuidade, isto é, prevendo que o fluxo deste vetor através de uma superfície fechada esteja diretamente ligado à variação de energia contida ali.

Ao imaginarmos, por exemplo, ondas provenientes da região interna desta região fechada, é natural associarmos a direção e sentido do vetor que representa o fluxo de energia com a direção de propagação das OEM’s.

Entretanto, exatamente por se tratar de um campo vetorial definido por este produto entre os campos e , é possível que o vetor  possua componentes de um campo vetorial solenoidal, i.e., imaginando uma superfície fechada sobre a OEM, na qual em uma parte da superfície as componentes de emergem, enquanto em outra região da mesma superfície a penetrem, resultando assim que o fluxo total seja nulo. Desta forma, se o produto  produz componentes que não são paralelas à direção de propagação de uma OEM, a característica principal de conservação de energia ainda deve ser preservada.

Estas ondas são muito mais comuns do que pensamos e, muito frequentemente, apenas casos ideais permitem aquela primeira construção de um vetor paralelo à direção de propagação. Estes feixes tem sido tema de pesquisa efervescente nas últimas décadas devido à possibilidade de estruturação de perfis da frente de onda de feixes óticos através da reflexão em dispositivos de cristal líquido, muito similares aos presentes nos monitores e telas de cristal líquido [1].

Outros aspectos básicos relacionados ao momento angular orbital dos campos das OEM ao estado de polarização desses campos das OEM passaram a ser intensivamente investigados devido à possibilidade imediata de sua utilização em diferentes aplicações. Entre essas podemos citar:

– A capacidade de utilizá-los como pinças ópticas (Prêmio Nobel de Física de 2018 para Arthur Ashkin [2]), ou seja, utilizar tanto o momento linear de feixes para “empurrar e puxar” partículas na região do gradiente dos campos, assim como “girá-las” através da transferência de momento angular [3].

– Em telecomunicações, por conter informação adicional ligada a este outro grau de liberdade das OEM [4].

[1] Sonja Franke-Arnold and Neal Radwell, “Light Served with a Twist” Optics & Photonics News, junho de 2017. https://www.optica-opn.org/home/articles/volume_28/june_2017/features/light_served_with_a_twist/ .

 [2] https://www.nobelprize.org/prizes/physics/2018/ashkin/facts/ .

[3] Miles Padgett: Optical tweezers and twisted beams of light, SPIE, Photonics West, 2012, https://www.youtube.com/watch?v=2hdKXMRKSY8 .

[4] Alan Wilmer – Orbital Angular Momentum Multiplexing, DanishCA Photonics Workshop, 2014, https://www.youtube.com/watch?v=D40gKUWwx7A .