Temperatura da sonda Parker em sua máxima aproximação do Sol
21 de dezembro, 2021 às 15:51 | Postado em Astronomia, Radiação, Termologia, termodinâmica
Respondido por: Prof. Fernando Lang da Silveira - IF-UFRGSProfessor Lang
Fui seu aluno há mais de uma década em uma disciplina de Termodinâmica das engenharias (FIS183) e acompanho as suas postagens no Pergunte ao CREF. O sr. estimou em aula a temperatura que uma placa no espaço interplanetário, tão distante do Sol quanto a Terra, teria caso recebesse a radiação solar. Lembro que tal temperatura era compatível com a temperatura na superfície da Lua iluminada pelo Sol. Este exemplo da aplicação da Lei de Stephan-Boltzmann me foi marcante, bem como toda a disciplina.
Pergunto-lhe se é possível estender aquele raciocínio para se estimar a temperatura que o escudo térmico da sonda Parker atingiu neste último periélio há alguns dias.
Agradeço antecipadamente a sua resposta assim como a oportunidade de ter aprendido muito com o senhor.
Abraços e bom final de ano!
Recordas de uma bela aplicação da Lei de Stephan-Boltzmann (LSB) que trata da radiação térmica do corpo negro. A LSB relaciona a radiância R, isto é, potência eletromagnética irradiada por unidade de área, de um corpo negro com a sua temperatura absoluta T , ou seja,
![]()
onde σ é a constante de Stephan-Boltzmann e vale 5,670×10−8 W/(m2.K4).
Como a superfície do Sol emite aproximadamente como um corpo negro na temperatura 5777K, encontra-se a potência eletromagnética total irradiada P multiplicando-se R pela superfície do Sol (o raio do Sol é 696.340km ou 6,9634×108m) encontrando-se
P = 3,848×1026W . (2)
Esta potência, emanada da superfície do astro, distribui-se sobre uma superfície esférica com raio cada vez maior conforme a radiação se propaga no espaço interplanetário. A uma distância d do centro do Sol esta potência está distribuída sobre uma superfície esférica com raio d. A intensidade da radiação solar I a esta distância d é encontrada dividindo-se P pela área da superfície esférica com raio d, ou seja,
![]()
Se a radiação solar incidir sobre uma placa no espaço interplanetário, sendo a área A da placa, ela será parcialmente absorvida dependendo da emissividade ϵ da superfície da placa. A emissividade é uma constante adimensional que vale 1 para o emissor ou absorvente perfeito (o corpo negro) e zero quando a superfície reflete perfeitamente a radiação ou não a emite. Superfícies metálicas possuem baixa emissividade, sendo usadas quando se deseja refletir a radiação incidente ou reduzir a emissão térmica. No seguinte endereço encontram-se valores para a emissividade de diversos materiais: Engineering Tool Box.
Enquanto a placa absorve radiação a sua temperatura aumenta e concomitantemente a placa irradia mais. A temperatura da placa atinge um valor constante quando toda potência eletromagnética absorvida é igual a potência eletromagnética irradiada.
A potência absorvida, na superfície da placa voltada para o Sol, é igual ao produto da emissividade ϵ pela intensidade da radiação solar (dada pela equação 3) e pela área A dessa superfície, ou seja,
![]()
A potência emitida pela placa é o produto da equação 1 pela emissividade e pela área total das duas superfícies da placa (2A). Ou seja,
![]()
Conforme notado anteriormente a temperatura da placa se estabiliza quando as potências dadas pelas equações 4 e 5 são iguais. Então, igualando-se as duas equações e isolando a temperatura se encontra
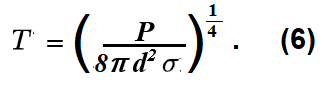
É importante notar que esta temperatura extrema independe da emissividade da placa. Entretanto quanto menor é a emissividade, menor é a potência irradiada na região de sombra da placa. Em um escudo térmico deseja-se minimizar a potência irradiada para trás do escudo e portanto o escudo deve ser constituído por um material com baixa emissividade (alta refletância). Conforme notado anteriormente superfícies metálicas apresentam tal característica, por exemplo, o mylar aluminizado com emissividade igual a 0,04, foi utilizado nas missões Apollo para blindagem térmica de módulos que desceram na Lua.
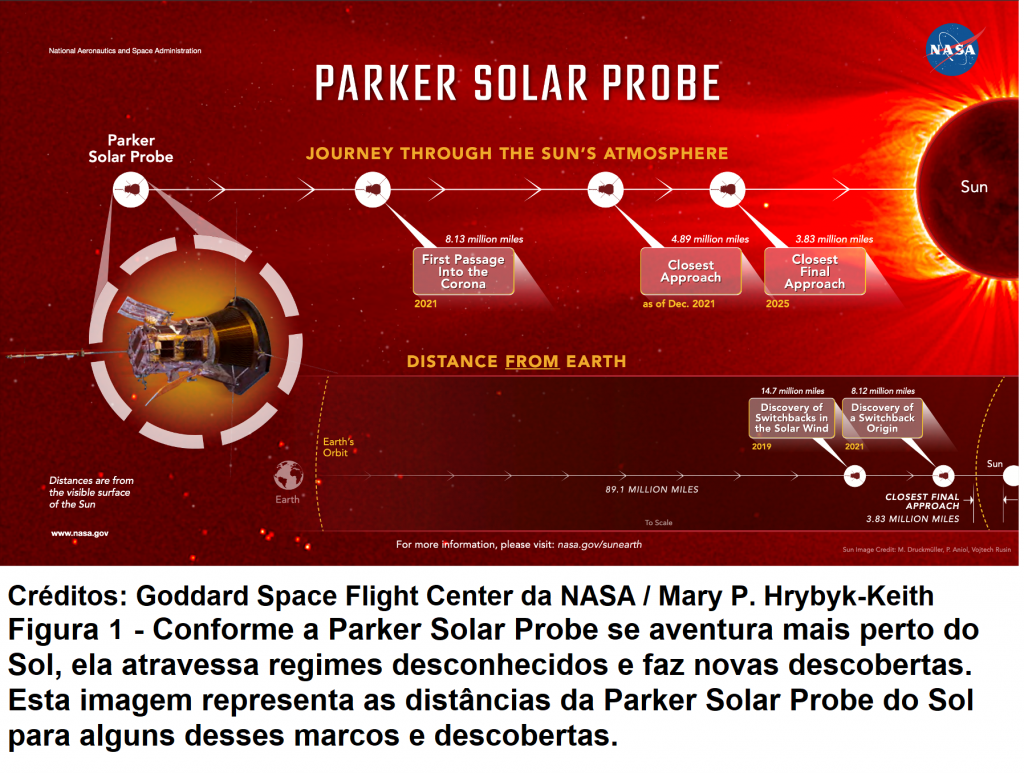
Se na equação 3 a distância d =1,4968×1011m (distância Terra-Sol), encontra-se que a intensidade da radiação solar I é 1370W, conhecido este valor como a constante solar. E quando nesta equação se coloca d =6,86×109m – que é a distância de máxima aproximação do Sol para a Sonda Solar Parker em sua passagem final por perto do Sol em 2025 (conforme representado na Figura 1) – a intensidade da radiação solar I resulta em 651000W, portanto 475 vezes mais intensa do que na órbita da Terra.
Usando-se a equação 6 para se estimar a temperatura do escudo térmico da Sonda Parker em máxima aproximação do Sol se encontra T=1550K ou cerca de 1300°C. Este resultado é consistente com as notícias relativas à passagem de 21/11/2021 por perto do Sol, “tocando” o astro. O escudo térmico propicia que mesmo nesta situação extrema, a temperatura na região por ele protegida se situa em torno de 30°C.
“Docendo discimus.”(Sêneca)

Qual é o ponto de fusão do mylar aluminizado?
Vide Mylar.