Coincidências de datas de aniversário
1 de agosto, 2017 às 14:45 | Postado em Estatística e probabilidade, incertezas experimentais, Matemática
Respondido por: Prof. Fernando Lang da Silveira - www.if.ufrgs.br/~lang/Professor Lang
Sempre que posso acompanho suas postagens e as indico aos meus alunos. Agradeço-lhe por repartir seu conhecimento.
Em um programa do Discovery Science, Um em Um Milhão, afirmaram que em um grupo cerca de 25 pessoas já há uma probabilidade elevada de existir duas delas com a mesma data de aniversário. Eu imaginava que tal probabilidade fosse baixa e a estimei em menos de 10%. O sr. poderia comentar sobre o tema? Muito obrigado!
Em um grupo de 25 pessoas tomadas ao acaso a chance de haver uma ou mais coincidências de datas de aniversário é superior 50%. Este é o conhecido “Paradoxo dos aniversários”, tratado em muitos textos e sítios da internet.
Vou apresentar a seguir a solução do problema que pode assim ser enunciado: Qual é a probabilidade de haver uma ou mais coincidências de datas de aniversário em um grupo de n pessoas?
A solução do problema começa por se calcular a probabilidade de não haver coincidências de datas de aniversário em um grupo de n pessoas. Esta é dada pelo seguinte produtório
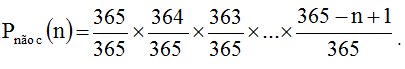
As possibilidades de haver ou não haver uma ou mais coincidências são mutuamente excludentes. Assim sendo a probabilidade de haver uma ou mais coincidências de datas de aniversário em um grupo de n pessoas é dada por
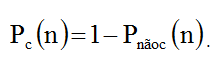
A tabela 1 apresenta para alguns valores de n as duas probabilidades.
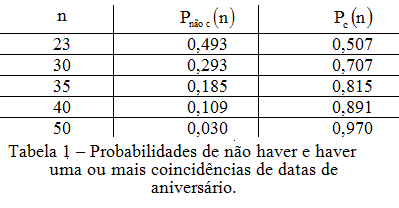
Assim se observa que em um grupo de 23 pessoas a probabilidade de que haja duas ou mais pessoas com datas de aniversário coincidentes já é maior do que 50%. Em um grupo de 50 pessoas é muito provável (97%) que existam duas ou mais pessoas com datas de aniversário coincidentes.
Relatarei agora uma história acontecida nos anos 80 do século passado com um aprofundamento do problema das coincidências das datas de aniversário.
Eu frequentava uma vídeo locadora de um ex-aluno de engenharia da PUCRS, o João. Como ele era muito interessado em física e matemática, não raro conversávamos sobre tais temas. Um dia lhe fiz o seguinte questionamento:
Em um grupo de 40 pessoas tomadas ao acaso, tu apostarias que há indivíduos com a mesma data de aniversário?
Ele de imediato me respondeu dizendo que não apostaria pois era improvável que em grupo de 40 pessoas houvesse coincidências de dias de aniversário, estimando tal probabilidade em aproximadamente 10%. Eu então lhe apresentei os cálculos e conclui dizendo que ele deveria apostar na coincidência pois a probabilidade era cerca de 89%.
O João então me disse:
Tá bom Fernando, eu entendi o cálculo! Mas quero fazer um teste sobre isso. A listagem de meus clientes é por data de ingresso na vídeo locadora, portanto nada tem a ver com seus aniversários. Vou tomar então os 40 primeiros clientes e verificar se há coincidências. Depois repetirei para os próximos 40 clientes e assim por diante.
Passados alguns dias retornei e o João me disse:
Fernando, estou convencido! Pretendia verificar em muitos grupos de 40 pessoas a existência de datas de aniversário coincidentes. Quando cheguei ao oitavo grupo parei pois em todos eles havia coincidências. O mais surpreendente ainda é que em apenas dois grupos havia somente duas pessoas com a mesma data. Nos outros seis grupos encontrei três e até quatro pessoas cuja data de aniversário coincidia com outra pessoa do grupo.
Eu também me surpreendi com o fato de haver mais do que duas datas coincidentes pois toda a literatura que já havia lido sobre o tema apenas apresentava os cálculos que mostrei anteriormente. Não encontrei nenhuma referência sobre distribuição de probabilidades das coincidências. Ou seja, até ali eu somente sabia ser muito provável ocorrer duas ou mais pessoas com mesma data de aniversário.
Minha abordagem subsequente foi “experimental”, simulando vinte mil grupos de 40 datas de aniversário com distribuição uniforme, usando o Método de Monte Carlo, computando em cada grupo a quantidade de datas diferentes. Representei em um histograma (figura 1) os vinte mil resultados.
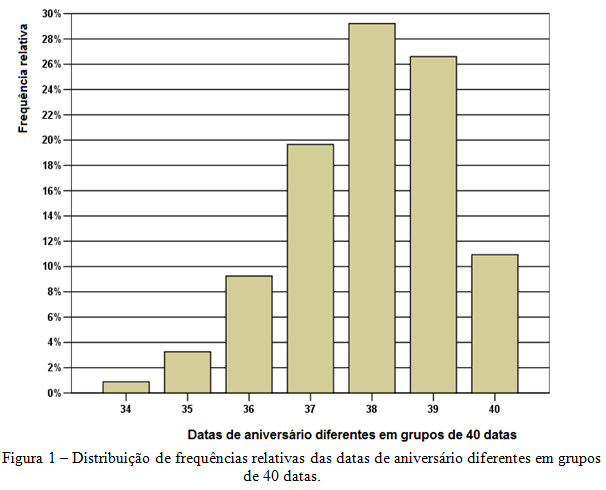
Conforme a expectativa baseada na tabela 1 ocorreu apenas 11% de datas completamente diferentes, ou seja, a probabilidade de haver uma ou mais coincidências é 89% nestas simulações. O máximo da distribuição de datas diversas aconteceu em 38 datas (a moda da distribuição é 38 datas diversas), portanto a probabilidade de existir três datas de aniversário coincidentes é maior (29%) do que apenas duas datas idênticas (27%). Mesmo coincidências maiores do que três possuem probabilidades não desprezíveis conforme o histograma indica.
Assim sendo os achados dos João em apenas oito grupos de 40 datas são consistentes com a simulação, revelando que de fato é provável (62%) haver mais de dois sujeitos com datas de aniversário coincidentes em um grupo de 40 pessoas.
Tomei posteriormente a listagem com quase cem mil datas de nascimento de vestibulandos da UFRGS nos anos 90 e os separei em grupos de 40 datas de aniversário, adotando a mesma metodologia da simulação. Obtive 2454 grupos, computando em cada um deles o total de dias diferentes de aniversário. O resultado se encontra representado no histograma da figura 2.
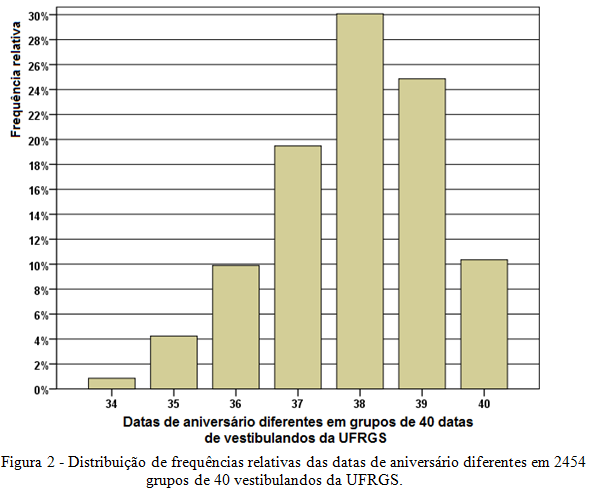
O histograma mostra frequências relativas muito semelhantes a aquelas encontradas na simulação da figura 1, corroborando também as probabilidades da tabela1.
Disponibilizo um texto com outros histogramas no ResearchGate.
“Docendo discimus.” (Sêneca)
Visualizações entre 27 de maio de 2013 e novembro de 2017: 1207.
